知名人物陆启铿人物简介

Posted 2022-04-04 数学

篇首语：努力到无能为力，拼搏到感动自己本文由小常识网(cha138.com)小编为大家整理，主要介绍了知名人物陆启铿人物简介相关的知识，希望对你有一定的参考价值。

知名人物陆启铿人物简介

·陆启铿

陆启铿，数学家。在多个复变数函数论方面作出突出贡献，研究了施瓦茨引理及一些解析不变量，建立了典型域的调和函数论 (与华罗庚合作); 证明常曲率有界域解析等价于球而引出了国际上称之为的 “陆启铿猜想”，提出了典型域的热核表达式等。在关于规范场与纤维丛的关系方面亦有创见。他还在培养年轻数学家方面作出了贡献。

中国科学院院士陆启铿，是一位多复变函数论及数学物理学家。他做的主要工作有： H.A. 施瓦茨 (Schwarz) 引理及一些解析不变量研究; 典型域的调和函数论 (此题与老师华罗庚合作); 典型流形与典型域; 证明常曲率的有界域解析等价于一球及由此所引出的 “陆启铿猜想”; 他以显式给出了典型域的全系解析不变量和热核表达式; 证明Cn中有界域D若具有全纯截曲率为常数的完备的伯格曼 (Bergman) 度量，则D一定双全纯等价于超球，而且此常数是-2/(n+1)，此结果被人们称为 “陆启铿定理”。

此外，他还在数学物理方面阐明了规范场 (即杨-米尔斯(Yang-Mills) 场) 与微分几何中纤维丛的关系，这是研究规范场的基础。例如他在1972年就写了一份纤维场与规范场的讲义，并在1974年首先在中国《物理学报》发表了相应的文章，特别他把数学微分几何中有关名称与物理学杨-米尔斯场中相应名称与记号一一列表指明，这一首创性工作是重要的。在相隔18年之后，他于1992年证明，自对偶规范场对于四维的洛伦茨(Lorentz) 流形必为零，即只有平联络，这里曾指明M.F. 阿蒂亚(Atiyah) 在规范场方面的理论不能平行推广于物理上常用的洛伦茨流形，必须另作考虑，对非线性研究的需要做了促进工作。这是中国现代数学家在上述问题中作出奠基性或经典性的贡献。

不畏病残，半工半读成就学业

陆启铿祖籍是广东省顺德县龙江乡。父亲陆子骥，母亲梁志雅。祖父是当地殷实商人，到父亲一辈时因子女多和社会经济不景气而家道中落。1938年日寇侵占广东，陆启铿随父母兄姐妹全家6人逃难到澳门时，已成为住贫民窟的穷人了。这样，他小学未毕业即告失学。

当时，他有位堂姐在澳门上中学。几年中，陆续借了她的从小学到初中的全部课本，自学了全部课程，1942年以同等学历考取澳门中山县联合中学高中一年级。他从小患小儿麻痹症，不利于行，疾病给他带来许多不便。这种极不利的条件，却养成了他刻苦努力、专心思考、重视理解和记忆等做一个科学家的基本品质。由于入学考试成绩和学习优秀，他获得了清贫奖学金。1943年转学到澳门中德中学。该校特别重视德文和数学，每学期都设有这两门课的奖学金。陆在班上总是一个人兼得这两项奖，从而获得免交学杂费等的荣誉。

1945年抗日战争胜利时陆启铿高中毕业。那时中山大学刚复员搬回广州，当时最先招生的是先修班，陆启铿以第一名被录取。他知道家贫供不起生活费，没等考试揭晓便到新会县桐井乡中心小学去教书了。

1946年夏，陆考取了中山大学数学天文系。虽说经过了1年工作，积攒了一点维持短期生活的钱，但要维持大学几年的学习则是很不够的。于是从这以后，他开始了半工半读的大学生活，每周四晚上坐火车去佛山，为私人补习英文、数、理、化，星期一早上赶回学校。暑期更是全部用来为各种补习班教课。这种情况一直继续到1950年毕业。由于他品学兼优，被留校当助教。当著名数学家、学部委员华罗庚从陆的毕业论文《模函数》中看到了作者的才能后，便接受他到中国科学院数学所筹备处当第一批研究实习员。由于学校舍不得放他走，1951年才让他到数学所报到任职。

陆启铿1962年与张木兰结婚。张木兰是北京市中学优秀数学教师，长期担任学校数学教研组长，她教的学生中有几人曾在北京市中学生数学竞赛中获奖。由于陆启铿行走不便，她长期为家庭付出了比一般主妇更多的劳动，让陆启铿潜心于数学研究。他们生有一子一女。

在华罗庚指导下成长

华罗庚对学术工作和对学生的要求都很严格。20世纪50年代前期清华大学思想改造运动中，一些人对科学精神认识不深，极 “左”、过火，引起华罗庚的不快，导致胃大出血。但这没有使他退缩，他身体稍好后，就指导陆启铿读一本模函数的书，叫陆启铿每看完一章即向他报告。报告令他满意后，他给陆启铿??个题目，这就是陆启铿在华罗庚指导下完成的第一篇论文《A函数的富氏系数》。这也是陆启铿发表的第一篇论文《A函数是模函数的一种》。陆启铿回忆： “那个时候，我年轻劲头大，华先生写书叫我帮他整理，晚上开夜车，早上当然起得晚些了。当时华先生住清华园，清早想到什么问题，不时到我的宿舍敲门，把我从床上叫起来，和我讨论。华老那种一工作起来什么都不管的投入精神，对我起了潜移默化的作用”。

数学研究是一项需要精力高度集中，不断系统持续地冷静思索和反复运算，以寻求最优解答表达的过程，没有安定的小气候是难于做出成果的。可20世纪50年代前期大小政治运动持续不断，不能安下心来进行创新研究。直到1954年才出现有较安静一点的研究条件，陆启铿用1年多的时间系统整理出 “多复变函数与酉几何” (酉几何现叫Hermite几何)。这篇近100页的论文，奠定了他在数学领域中作为一个多复变函数论专家的基础。

20世纪50年代前期，凯勒 (Kahler，亦译为卡勒) 几何及伯格曼度量在国际上刚开始受到重视，专门介绍凯勒几何的书还没有。华罗庚建议他做这一工作。不久，陆启铿写出文章第一次探讨了用伯格曼核函数构造正交系，计算出各种典型域的测地线等问题，他还把与华先生讨论时提到用矩阵方法去处理凯勒几何的新研究方法也很好地用上。1954年，陆升任助理研究员。从此，陆启铿开始了独立或与他人合作的研究创新道路。一个大学毕业生仅用三四年时间能迅速达到这种水平，成长是很快的。

施瓦茨引理及解析不变量

中国科学院数学所是我国开放得最早的研究所之一，50年代前期即陆续有外地学者、专家来所讲学或进修。1954年陆启铿和当时来所进修的厦门大学钟同德合作，研究多复变函数的普里瓦洛夫 (Привалов) 定理，完成了论文 “普里瓦洛夫定理的推广”。其公式可应用于CR流形中，能表示各种形式的推广，带有典型性。我国数学家李国平院士与前苏联加霍夫 (Гахов) 学派认为这是创新工作，给予颇高评价; 前苏联一学者做博士论文，特写信来请翻译该文。可惜当时未能翻成外文在国际数学界交流，致使一项先进工作未能得到应有的普遍承认。直到20年后，美国R. 哈维 (Harvey) 与H. B. 劳森 (Lawson) 在《数学年鉴》(Annal. of Math.，1975) 重新发现此公式并作类似表述。

陆启铿在多复变函数领域首次得到国际数学界同行普遍认可的工作，是1956年完成的有界域的施瓦茨引理及由此引进的??些解析不变量的研究。这是用积分与伯格曼核函数的性质来证明施瓦茨引理，首次在多复变函数论中指出施瓦茨引理与曲率的关系，也由此进一步指出所产生的那些解析不变量，可用以判别两典型域是否等价的问题。由此可立即得出卡拉泰奥多里(Carathéodory) 微分度量 (1967年由H.J. 赖芬 (Reiffen) 引进)，小于或等于伯格曼度量。

陆启铿在一次谈到自己在科学研究中发现新苗头的体会时说： “有些问题很多人都以为没有问题，放过去了，可是你只要认真思索，不放过疑点和难点，进而去多方面找一些解题方法，总是会有所收获的，许多创新也常从中引发。例如第一个获菲尔兹 (Fields) 奖的L.阿尔福斯 (Ahlfors)，他曾提出把一变元代替函数的定理推广到高维，就能把单复变函数的几何理论推广到多复变情况。”

正是由于陆启铿引进了一些不变量，使施瓦茨引理从原来论述并不完全发展成处于多复变函数领域中一个极重要地位。前苏联1948年出版一本多复变函数论的书 (作者В.Л.Фукс)，对施瓦茨引理没有作什么论述，但等到1963年再版时，就以较多篇幅把陆启铿的结果全补写进去。也是大约20年后，美国有个叫K. T. 哈恩 (Hahn) 的人最多只能说他做了雷同于陆的工作，当然所用的符号和有些表述文字不同，但居然因此而出名。^①

华罗庚很欣赏这个勤奋的学生陆启铿的数学才能，1956年开始与他合作写了几篇典型域的调和函数论的文章。这是中国华罗庚学派中，华罗庚自己在50年代起和学生合作的开始。那时候，华罗庚除任数学所所长外，还兼任计算机研究所筹备主任，有许多学术上的社会工作，如制订12年数学远景规划等等，实在忙不过来，因而把自己开了个头的课题研究找陆启铿来合作完成。这些工作于1958年完成，所写出的总结论文，成为50年代一系列重要数学工作的概括，刊登在纪念建国10周年的英文?中国科学》特刊上。他们在这段时间把典型域的调和函数理论较完整地建立了起来，构造泊松 (Poisson) 核来解决这些域的狄利克雷 (Dirichlet) 问题，并详细研究了这些域的边界的几何结构，通过引进缝空间的概念，得出了在缝空间的链上的极大值原理，这些均已成为这个理论的经典工作。

1955年，北京大学程民德教授在和华罗庚的交谈中，认为中国数学家中搞多复变函数论的人太少，而这个领域又很重要，因而提议请陆启铿到北大数学系为高年级学生开这一专门课程。北京大学数学系还专门在四年级中挑选10人，并把他们大学毕业时间由5年延长到6年。1962年这10人毕业，现在已大都在全国各地成为我国多复变函数论的研究骨干，其中包括有才华但不幸早逝的钟家庆教授。这门课的讲义已印成《多复变函数引论》和《典型流形与典型域》两本书发表。前者系统介绍这一领域的工作，后者则是陆启铿本人研究工作的总结。50年代中期以来，前苏联数学界同行对陆启铿的工作有越来越深的印象，1961年曾邀请陆参加全苏函数论会议，并安排会后请他到罗斯托夫大学讲学两周。后由于两国关系紧张，计划未能实现。

拓广勒雷公式

法国数学界权威，法兰西科学院院士J. 勒雷 (Leray)，直接继承了著名数学物理学家H. 庞加莱 (Poincaré) 的一些工作，他对柯西 (Cauchy) 问题有一系列著述。1964年，数学所研究员吴新谋鉴于勒雷工作的重要和提出了许多新问题，因而组织了一个勒雷文章的讨论班，陆启铿承担了勒雷的一篇在1959年新发表的长达100页的关于 “复流形上的微积分” 文章的报告。在深入分析中，陆启铿发现勒雷建立的柯西-范塔皮公式十分重要，但作者自己却还未很好拓广。因而陆在他的论文《关于CauchyFantappié公式》中，指出由该公式可推导出华罗庚的典型域的柯西公式，证明苏联A.A. 阿京伯格 (Акеберг) 在当时得出的一些柯西公式，可看作是法国F. 诺尔凯 (Norquet) 从柯西-范塔皮公式所推出的特例等，这些是陆启铿对勒雷提出的一个重要定理的实质性的发展，也是他最先用勒雷公式于积分表示的工作之一。在诺尔凯的讨论班文集中曾多次引用此文，这项工作先后于1965年和1966年发表了论文摘要和全文，美国同行很快把陆启铿的文章译为英文登载在他们出版的《中国数学》 (Chinese Mathematics) (1966) 上。

1987年勒雷应南开大学邀请来中国访问，老教授在北京停留时作了工作报告，谈到他建立的柯西-范塔皮公式 (实际是勒雷公式)，盛赞苏联学者创造性的发展。当陆启铿听完讲演，把美国1966年翻译他的文章的英文复印本送给勒雷，老人看后表现异常惊奇。他说没有料到他1959年刚做出的工作，中国学者在1963年就做出了创造性的应用，这个最早独具慧眼并首先发展他的工作的，竟是一个中国年轻同行。1988年，陆启铿访问瑞典，勒雷的学生以巴黎第六大学数学系名义邀请陆启铿去巴黎访问一周，作两次学术报告。首次报告会在法兰西学院庞加莱研究所进行。欧美科学家是极重视尊师重道的，当82岁老人勒雷缓步走进教室时，全场50多人都起立致敬。当勒雷坐上第一排时，原坐一排的学者退坐到第二排，显示了法国科学家对有贡献的前辈的尊敬。当报告结束，勒雷第一个站起来上前和陆启铿握手，感谢他首先对勒雷公式的重视和开拓，随后，他把自己手头仅有的一套全部论文的单行本送给陆启铿。从1988年起迄今，勒雷每年都给陆启铿寄来贺年片，显示老人把陆启铿视为自己学术上的知音。

陆启铿在1965年向数学所领导提出组织现代数学讨论班的建议，以使中国数学工作保持在世界数学有关领域的先进地位。吴文俊和张宗燧等很欣赏这一意见，并建议陆启铿第一个先讲微分几何与李群的关系。陆启铿共作了6次微分几何与李群问题的报告。讲义因 “文化大革命” 没能出版。70年代初期，国际上开始注意理论物理与微分几何的关系，但国内现代微分几何书籍缺乏，人们回忆起几年前陆启铿的微分几何与李群问题的报告，因而该讲义被一些单位复印，这是陆启铿在数学应用到理论物理上对中国学术界起的好影响的工作之一。

“陆启铿猜想”

陆启铿的一些工作走在各国同行前面，因而逐渐为外国同行注意。他引起世界数学界同行较广泛重视的工作是1966年发表在《数学学报》上的 “关于常曲率的卡勒流形”，证明伯格曼度量的酉曲率为常数的有界域必等价于一球。这篇有影响的文章立即被美国的英文《中国数学》翻译转载。随后不断引起一些数学家的研究讨论——在其他什么条件下，一有界域全纯等价于一球问题，由于文章提出伯格曼核函数有没有零点的这一有趣问题，1969年波兰一位数学家M. 斯卡里津斯基 (Skwarczinski) 首先称此为 “陆启铿猜想” (Bull. AMS，1969)，他当时举出一个反例，这样他便称伯格曼核函数没有零点的域为 “陆启铿域”。近20多年来，国际上不断有人论证什么域的 “陆启铿猜想” 成立，什么域的不成立。格林-伍 (Green-Wu) 与S. G. 克兰兹 (Krantz) 还把 “陆启铿猜想” 修正为有界的单连通的强拟凸域的伯格曼核函数没有零点。到1986年，R. P. 博斯 (Boas) 又同样举出一个反例，使问题的研究又深入了一步。总之，国际上对这个 “猜想” 的兴趣至今不衰。“陆启铿猜想”是50年代以来首先为各国承认的中国数学家提出来的第一个猜想。说起这个问题还是华罗庚首先告诉陆启铿的。原来有一次华老问他： “什么叫陆启铿域”，他回答说不知道，一查文献，才知道从1969年起国外一直断断续续有人研究这个问题。

规范场与主纤维丛的联络

在自然界，有时两个截然不同的事物之间，从外表上看去似无联系及共同之点，但在一些对新鲜事物极其敏感，熟悉它们各自本质机理，并敢于刻苦攻关的科学家的深入探索之后，竟能找出其中本质联系，从繁杂的迥异的表面现象中抓到科学研究中的主要数量关系，从而率先取得带经典性的成果。陆启铿就是从自己多复变函数论研究中有幸比自己的一些优秀同行能较好理解数学表达式中的物理概念，又比许多优秀的物理学家能较好地用数学语言表达物理学所要求的一些关键因子式，如拉氏函数中的质量项，等等。反映了 “寸有所长” 的特殊经验。

陆启铿在1992年获首届华罗庚数学奖的颁奖仪式上说过，他的一些成绩的获得，是由于有知识渊博的华罗庚老师，有老师为自己指定的多复变函数这个终身从事的主要研究方向，有一个当时全国最好的研究数学的环境，有不少著名数学家为他学习、借鉴提供最有利条件。他回忆： 50年代前期数学所内绝大多数研究人员都是夜以继日地全力去探索，晚上办公室灯火通明。吴文俊先生介绍微分流形与现在所称的大范围的微分几何; 冯康先生介绍广义函数论。他说，由于多复变函数论需要其他学科的知识，其中微分几何是重要的一种。他曾自己去读二三十年代出版的艾森哈特 (Einsehart) 的与

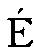. 嘉当 (Cartan) 的黎曼几何，但后一本书十分难念，例如这本书经常用到流形 (variete) 的概念，但他找不到关于流形的定义。所以他张量运算的技巧还可以，但对最基本的概念却不甚了了。听了吴先生的精辟的微分流形介绍以及德拉姆 (de Rham) 定理的证明，遂使他顿开茅塞。所以他的关于大范围微分几何知识的启蒙老师是吴文俊先生。冯庚先生的广义函数论的报告，对他也是一种启蒙。在此之前他不知道什么叫广义函数，因为L.施瓦兹 (Schwartz) 的广义函数论虽于1950年出版，但中国还未见到，而盖尔范德 (Gelfand)的广义函数论还未出版呢。

他说： “我不仅不是天才，我的能力最多只是平均水平 (average) 上下，但有幸处于当时一个相对优越的环境。这也不是说当时物质生活条件比现在好，像我工作7年之后才积蓄了足够的钱来买一台过得去的收音机来听音乐。那时候什么电视机、电冰箱我还没有见过。基础研究的成果未必与物质生活条件成正比。”

陆启铿缅怀一段使他成长而终身不忘的往事时说：“华先生在系统教导我研究模函数时，他要我一个人站在上面讲，他一个人坐在下面听，然后一点一点地提出问题，追问为什么，直到解释满意为止，采用了一师一生的形式专门指导。以此进行问学。”“每次我都是事先战战兢兢的小心准备，每一个细节都很好验算，以准备他问起来好回答。纵然如此，他总是会问一些意料不到的问题。这样我经常被吊在黑板上，十分狼狈。开始我很不好受，面子上很难受，但越往后我越觉得从这种训练中受益匪浅，我知道华先生在用言行教我知道什么是严谨与严密，什么是广泛联系和深入思考，以及如何才能把一个复杂的定理证明，分析为各个要素及找出关键所在”。

老师的教诲，有时是一言片语指点迷津。陆启铿回忆说：“华老对我的研究工作，无论在思想方法上还是在技巧运用上，在我的论文中是到处可见。50年代中期，我曾花了几年时间，想把单复变函数的施瓦茨 (Schwarz) 引理推广到多复变函数，花了许多力气，但还是要差一个与曲率有关的常数因子才能使证明成立。华老一听我这个结果，便说这个因子可能就是解析不变量。经华老一语道破之后，我果然很容易就证明它确是一个解析不变量，所以我在发表的文章中特别说明，这是由华罗庚教授??启发的Inspired (灵感)。不久，福克斯把这个结果放进他新出版的专著中，有的人称之为 ‘陆启铿不变量’，其实应该说是由华罗庚所启发的不变量。”

这种师生坦诚和无保留的教和学，进行传道、授业、解惑，在现今看来是很难能可贵了。使陆启铿在名师教育和自己努力之下，为中国数学重新立足世界数学先进之林中贡献自己的一份力量。

“文化大革命” 期间，中国科学界在极 “左” 思潮影响下，科研工作除与国防需要有关者外，差不多都被迫停止了。也许数学家的研究工具最为简单，只要资料、纸和笔，但那时候没完没了的 “触及灵魂” 的批判斗争会，搅得人静不下心来，到图书馆去看书也是犯禁令的。绝大多数的科学家是无法把需要冥思苦索的研究工作继续下去的，陆启铿当时也不例外。

有趣的是，在台风扫及的广泛不安定中，却在其中心有一个台风眼那样平静的小气候环境存在。陆启铿在当时中国动乱的大气候中，却意外地被卷置进一个安定小气候中，从而使他能充分利用这一难得机会，做出了跨数学和理论物理两个领域的创造性的工作。

20世纪60年代末期，受极 “左” 思潮严重影响，要批判爱因斯坦相对论，于是分别在上海和北京成立大批判组。陆启铿由于德文好又了解相对论，且思维敏捷缜密，平和近人，因而被挑选进北京的大批判组作资料调研工作。这个 “政治任务”意外地让他可以整天安心埋头在图书馆或家里，不受任何干扰研读资料和思索。他在这段时间可以夜以继日地对他所感兴趣的问题深思和求解。另一方面，这个大批判组集中了中国一批优秀的中青年理论物理学家，闲谈中使陆启铿机敏地捕捉到当时理论物理学界一些尖端问题。

20世纪70年代以来，物理学和数学的重新接近突出在两个问题上，一是规范场和纤维丛上的联络的关系，二是孤立子问题。特别是前者，由于相同的问题因不同学科以不同名词说明同一个概念，造成数学家和物理学家之间难以交流。陆启铿具有善于把表面看来不相关的事物联系起来，并发现其本质的能力，这能力需有极开阔的眼界和背景知识才能获得。在理论物理上的规范场与数学中的主纤维丛的联络这一重要问题上，陆启铿作为??个数学物理学家作出了重要贡献。^①

原来1972年7月间，诺贝尔物理奖获得者杨振宁第二次回国，他在北京大学对自己正在研究的规范场的积分表示作了报告; 在讨论中回答问题时，顺便提到国外有人说过规范场可能与纤维丛有关的一句话。这完全是一句介绍过去碰到的情况时无意中涉及的话，但却为陆启铿的有准备的头脑敏锐地捕捉住了。原来陆启铿在1959年就曾做过纤维丛联络论的工作，科学家对自己感兴趣的问题从来都是锲而不舍的。在当时有利的小气候中，陆启铿当然更不会放过。于是他夜以继日奋战两星期，终于弄清规范场就是联络，并列举出规范场与纤维丛两者相对应的关系，证明规范场的积分定义相当于用平行移动来定义的联络，写出了一份纤维丛与规范场的讲义，并在物理所与高能所作了报告。由于这是第一篇研究这个问题的经典性文献，因而这个讲义被一些大学复制多次，一时成为在理论物理学界流传的读物。有一些华裔年轻物理学家，一到中国便索取此讲义。此后陆启铿正式写出了这个问题奠基性论文《规范场与主纤维丛上的联络》，于1973年投稿，1974年刊登于新复刊的《物理学报》上。物理学因引进数学上的联络关系而拓宽了领域，数学则因规范场的反弹力而得到新的发展。

陆启铿在1972年油印稿的引言中写道：“试图向研究物理的同志介绍一下已经及将来可能与物理有关的纤维丛理论。这是??个困难的任务，并且是一个可能过于大胆的尝试。近代纤维丛理论的叙述，多是一个接一个的数学定义与概念像金字塔一样堆积起来的，这对习惯于从具体出发，并非从抽象定义出发的物理工作者，往往感到陷入迷宫一样，同时这也是长期来使本来彼此关系十分密切的数学与物理后来变得彼此隔膜的原因之一，微分几何产生的纤维丛概念不过是例子之一而已。但是20世纪70年代近代物理与近代数学理论的重新结合，似乎比想像得到的更快地来临”。

1975年，杨振宁在《物理评论》 (Physics Review) 上也发表了他的规范场与主纤维丛联络的论文。1980年，杨振宁在?今日物理》的一篇文章中谈到： “只是到了近年，物理学家才懂得规范场和纤维丛上的联络这个几何概念有密切关系”。1983年，杨振宁进一步解释说：纤维丛中可以 “把一个完整的流形切开，再巧妙地接起来，天衣无缝地归还原形。我在1975年懂了此中奥妙以后，真有叹为观止之感”。(杨振宁：《读书教学四十年》，三联书店北京重印，1987年)，这反映了数学家和物理学家在数学物理上改变了研究分离而开始走向研究的接近。

在一个被扭曲了的时代，中国科学家居然只要有一个不受干扰的小气候，就能做出很漂亮的工作，显示了中国科学家群体的深厚功底与工作修养。

有些人总羡慕别人有好机遇，碰到好问题从而做出好工作。其实，科学研究上的机遇固然不断存在，但却都是为长期作了很扎实准备工作的人才能获得。陆启铿如果不是在中学时对德文打下了牢实的基础，对他来说，这种 “文化大革命” 中意外出现的研究小环境，也是难以利用的。

他和中青年物理学家在一起合作，才使他做了数学、物理、天文学三门学科有意义的共同研究。

1986年，美国韦伯 (Weber) 第一次发表了探测到可能是引力波事件的实验报告，1969年起引起欧美研究的热潮。陆启铿和年轻的科学家刘煜奋、邹振隆、郭汉英等合作，也开展这个问题的研究。陆提出用旋量分析方法，突破了当时理论物理学家用传统的经典分析方法为主的做法，做了一些有特殊见解的引力波场方程的工作。著名理论物理学家朱洪元院士称赞和支持这种跨学科合作，认为扩大了科学家的视野和认识的探入。1971年，1970年的诺贝尔物理奖获得者H. 阿尔芬 (Alfvén) 来中国进行友好访问，当他作为一个天体物理学家访问北京天文台时，惊奇地听到陆启铿做的引力波工作报告，因为多学科合作和用创新方法的研究，当时在欧美也很少见到。

不幸的是，随着以后政治气候的变化，这一块小小的安静环境也失去了，他们这方面的工作，像 “文化大革命” 中毁掉的许多有苗头的工作一样，不能再继续下去了。

锲而不舍，成果不断

1978年，陆启铿才有机会恢复长期从事的多复变函数论的研究。1980年他在美国访问讲学时，接到华老给他的信，提议他担任数学所副所长。他回国后和华老谈，“希望副所长采用民主投票选举的办法，选上我那就只好接受”。华老愉快地接受了学生兼同事的建议，召开数学所助理研究员以上人员参加的选举会。结果陆启铿以三分之二的多数当选。这一新方法被科学院领导知道后，曾建议在其他一些所推广。此后华老由于年事渐高，希望更好地把自己精力用在研究工作上，因此委托陆启铿主持全所日常工作。

1978年迄今，他已把20多年前由自己开拓的有界域的施瓦茨引理的著名工作，进一步从低阶微分推广到高阶导数的估计工作; 与他的学生陈志华及美籍华裔学者郑绍远一起推广施瓦茨引理到适合一定曲率条件的完备的凯勒流形上; 他又证明截曲率为非正的凯勒流形的截曲率平方，必小于或等于这两个截面的全纯截曲率之积。这些结果都是完善施瓦茨引理的关键工作，文章都发表在《中国科学》上。

1982年，陆启铿与理论物理学家郭汉英、吴可一起发展非线性规范场工作。另外陆启铿最近论证非线性规范场的拉氏函数中可以有质量项，显示与通常的线性规范场不一样。

1986年开始，陆启铿开始热核的研究，经历10年工作才告一段落。他对非紧致对称空间的热核，已经系统地具体地构造出来，其中一部分工作则是和他的同事并有博士研究生参加下取得的。国际上对陆启铿有关这方面的工作，从论文发表后即陆续有正式评价，《数学评论》 (Math. Review，1992年) 认为他的这些文章是重要的，是 (帮助引导深入研究的) 有用工作。他现又开始紧致对称空间的特征函数等工作。

同时，陆启铿继续应用勒雷的柯西-范塔皮公式作了开拓和发展，如一类多项式域的

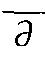-方程解的积分表示。这项工作，前苏联大百科全书第七卷上，数学家G. 亨金 (Henkin) 认为此方法行之有效。

陆启铿研究工作的总结性专著《典型流形与典型域新篇》于1997年出版。

从20世纪80年代开始，陆启铿与许多国家著名数学家、物理学家都有来往，多次出国讲学、研究、访问和参加国际数学家、数学物理学家的学术会议。其中时间最长的一次是在1984至1985年，美国普林斯顿高等研究院邀请陆去该院从事多复变的深入研究。40年代以来，美国普林斯顿高等研究院是新的世界数学和理论物理中心之一。

陆启铿由于从小患小儿麻痹症，双脚残疾，比他的导师华罗庚更不利于行，而且家境贫寒，依靠半工半读念完大学。他的毅力和勤奋，对新鲜事物极其敏感，善于联想和发掘事物之间的内在联系的能力，终于使他成为优秀科学家。他常对学生说： “我不是天才，做出一些工作完全是下苦功的结果。” “学报上发表的论文也许是吸引人的，但实际的研究过程却是夜以继日绞尽脑汁去苦思的过程。”

一个科学家有时作出某个发现，也许可归因于偶尔机遇，但接二连三不断作出好成绩，却带有一定的主观努力的必然因素。陆启铿便是如此。他治学中最宝贵的经验是坚持 “锲而不舍” 的奋斗精神。“勤奋出天才”，每一位有成就的科学家常因勤奋而才能更为突出，陆启铿的数学生涯再一次证明了这个真理。

简历

1927年5月17日出生于广东省佛山市。

1946—1950年在中山大学数学天文系学习，毕业后留校工作。

1951—1998年在中国科学院数学研究所工作，历任助理研究员，副研究员，研究员。

1980年当选为中国科学院院士。

1980—1983年任中国科学院数学研究所副所长。

1992年获华罗庚数学奖。

2001年获何梁何利基金科学与技术进步奖。

主要论著

1 陆启铿. 多复变函数与酉几何. 数学进展，1956，2 (4)： 587—662

2 陆启铿，钟同德.Привалов定理的拓广. 数学学报，1957，7 (1)：144—165

3 陆启铿. 多复变数函数的Schwarz引理. 数学学报，1957，7 (3)：370—420

4 陆启铿. 一个解析不变量及其示性作用. 数学学报，1958，8 (2)：243—252

5 Lu Qikeng. Schwarz lemma and analytic invariants. Scientia Sinica，1958，7 (5)： 453—504

6 陆启铿. 对于GL (n，R) 的连续表示之无穷小联络的表式. 科学记录，1959，3 (7)： 232—235

7 Lu Qikeng. Explicit formula of the infinitessimal connection for a continuous representation of Gl (n，R). Science Recons，1959，3 (7)：296—300

8 陆启铿. 链空间与极值定理. 科学记录，1959，3 (7)： 228—231

9 Lu Qikeng. Slit space and extremal principle. Science Record，1959，3(7)，289—294

10 Lu Qikeng (with L. K. Hua). Theory of harmonic functions in classical domains

11 陆启铿. 十年来的中国科学—数学—多复变函数部分. 十年来的中国科学—数学，北京：科学出版社，1959，202—213

12 Lu Qikeng. A study of the theory of functions of several complexvatiables in China during the last decade. Scientia Sinica，1959，8 (11)，1230—1237 (此文转载于美国数学会刊物 “Notice”，1960.)

13 陆启铿 (与许以超). 关于可递域的一个注记. 数学学报，1961，11(1)： 11—23

14 陆启铿. 多复变数函数引论. 北京：科学出版社，1961

15 Lu Qikeng. On a class of homogencous complex manifolds. Scientia Sinica，1963，11(6)： 723—751

16 陆启铿. 扩充空间的椭圆几何. 数学学报，1963，13 (1)： 49—62

17 陆启铿. 关于 “扩充空间的椭圆几何” 一文的补注. 数学学报，1963，13 (2)： 314

18 陆启铿. 一个二次矩阵方程之解及其几何意义. 厦门大学学报，1963，10 (2)： 89—134

19 陆启铿. 典型流形与典型域. 上海：上海科学技术出版社，1963

20 Lu Qikeng. A note on the Cauchy Fantappie formula. Scientia Sinica，1965，14 (1)： 624—625

21 Lu Qikeng. On the complete Kahler manifolds with constant，unitary curvature. Scientia Sinica，1965，14 (6)： 921—927

22 陆启铿. 关于常曲率的Kahler公式. 数学学报，1966，16 (2)：269—281

23 陆启铿. 关于Cauchy Fantappié公式. 数学学报，1966，16 (3)：341—363

24 陆启铿. 规范场与主纤维丛上的联络. 物理学报，1974，23 (4)：249—263

25 陆启铿 (与邹振隆，郭汉英). 典型时空中的运动效应和宇观红移现象. 物理学报，1974，23 (4)： 225—238

26 陆启铿. 有限域解析映照的固有微分的估值. 科学通报，1978，23(3)： 146—149

27 Lu Qikeng. On the solution of the light curve of partially eclipsing binary system. Scientia Sinica，1978，21： 613—628

28 陆启铿 (与郑绍远，陈志华)，完备Kahler流形上的Schwarz引理.中国科学，1979，9： 849—856

29 Lu Qikeng. The estimation of the intrinsic derivatives of the analytic mappings of bounded domains. Scientia Sinica，1979，(2)： 1—17

30 Lu Qikeng (with C.H. Chen，Siu-yuen Chen). On the Schwarz lemma of complete Kahler manifolds. Scientia Sinica，1979，22 (11)： 1038—1048

31 陆启铿 (与殷慰萍). 一个变系数的波动方程的Cauchy问题之解. 数学年刊，1980，1 (1)： 115—128

32 陆启铿 (与陈东岳). 利用电子计算机进行公式处理. 计算机学报，1980，1 (3)： 193—201

33 Lu Qikeng. The right-translation invariant metric and variational principles on a principal fibre bundle. Proc. of the 1980 Conference of Theoretical Particle Physics，988—1005

34 Lu Qikeng. On the representative domain. Proceedings 1981 Hangzhou Conference，199—210，Birkhauser，1984

35 陆启铿. 微分几何学及其在物理学中的应用. 北京：科学出版社，1982

36 Lu Qikeng. On the Schwarz lemma of higher order. Proc. 1980 Beijing Symposium on Diff. Geometry and Diff. Equations. Vol.Ⅲ，1308—1381. Science Press&Gordan Breac，1982

37 Lu Qikeng (with Guo Han-ying，Wu Ke). A formulation of nonlinear gauge theory and its applications. Commun in Theor. Phys. (Beijing，China)，1983，2 (2)： 1029—1038

38 陆启铿. 关于Kahler流形截面曲率的最大和最小值的注记. 中国科学A辑，1983，11： 1006—1103

39 Lu Qikeng. The classification of the curvature tensors of the Kahler manifolds. Chinese Quart. J. Math.，1986，1： 15—32

40 Lu Qikeng. The Green forms and Cauchy formulas of a Kahler manifold. Chinese Quart. J. Math.，1987，2： 1—12

41 陆启铿 (与洪毅. 复射影空间中子流形的诱导度量. 华南理工大学学报 (自然科学版)，1988，16： 29—38

42 Lu Qikeng. Green form to intrinsic metric of a ball. Science in China(Series A)，1989，32： 129—141

43 Lu Qikeng. The heat kernel of a ball in Cⁿ. Chinese Ann. Math.，1990，11B (1)： 1—14

44 Lu Qikeng. The heat kernels of symmetric spaces. Proc. Symposium in Pure Math. ，1993，54： Part Ⅱ，401—409

45 Lu Qikeng (with Hong Yi). The heat kernel of the classical domain RI(m，n ). Proc. Mittag-Leffler Institute，483—500. Math. Notes，Princeton Univ. Press，1993

46 Lu Qikeng. On the Cauchy-Fantappie formula and the solution of

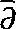equation. Diff. Geom. ，Symposium in Honor of Prof. Su Buchin on his90th Birthday，137—149，World Scientfic，Singapore，1993

47 Lu Qikeng. On nonlinear gauge field theory，Proc. Intern. Symp. on Inter face between Physics and Math. ，351—353，Singapore： World Scientfic，1993

48 Lu Qikeng. The horo-hypercircle coordinate and its application. Chinese Science Billetiv，1995，40： 92—95

49 Lu Qikeng. The mass term in the lagrangian of the nonlinear gauge theory. Singapore： World Scientfic，1995

50 陆启铿. 典型流形与典型域的新篇. 上海：上海科学技术出版社，1997.

注释

① 1979年陆去美国访问讲学,杨建平教授告诉说,哈恩和另一个美国人布比(Bubea) 还互争优先权,在加州柏克莱大学一次数学家报告会上,著名数学家丘成桐站起来当场指出: “你们讲的都不对,这个工作的结果是陆启铿的。” 由于该项工作重要,尽管两人证明的方法与步骤都与陆的相同,但都因此升为正教授。有趣的是,作出经典性贡献的陆启铿,则是文章发表了6年后,于1962年才升为副研究员。
① 1990年我国高科技中心的一次学术报告会上,物理学家侯伯宇就说上述问题的 “奠基人是陆启铿”。而早在1978年,我国著名物理学家钱三强曾在马列主义高级党校讲演中,称赞陆启铿在该领域中做了领先的工作。

知名人物 陆启铿人物简介

知名人物 陆启铿人物简介

·陆启铿

知名人物陆启铿人物简介

知名人物陆启铿人物简介