知名人物陈景润人物简介

Posted 2022-04-04 华罗庚

篇首语：生活不是上帝的诗篇，而是凡人的欢笑和眼泪。本文由小常识网(cha138.com)小编为大家整理，主要介绍了知名人物陈景润人物简介相关的知识，希望对你有一定的参考价值。

知名人物陈景润人物简介

·陈景润

陈景润，数学家，在解析数论领域作出杰出贡献。主要成就涉及表大偶数为素数与殆素数之和，殆素数的分布，华林问题等。

陈景润于1933年5月22日，生于福建省福州市。他的父亲陈元俊是一个邮政局职员，母亲于1947年即过世。由于父亲收入低微及家庭人口较多，所以家境相当贫寒。

陈景润在福州读完小学与中学。1949年至1953年，他就读于厦门大学数学系。大学毕业后，由政府分配至北京市第四中学任教。他因对教师这一工作很不适应而被辞退。厦门大学校长王亚南了解他的处境之后，于1955年2月将陈景润调回厦门大学工作。

那时，陈景润对数论产生了强烈的兴趣。厦门地处海防前线，时常有空袭警报，需到防空洞躲避。陈景润就把华罗庚的专著 “堆垒素数论” 撕开，放几页在身上，走到哪里，学到哪里。“堆垒素数论” 的第四章 “某些三角和的中值公式 (Ⅱ)” 是用华罗庚的方法来处理低次多项式所对应的三角和的中值公式。第五章 “维诺格拉朵夫的中值公式及其推广” 则是用维诺格拉朵夫方法来处理高次多项式对应的三角和的中值公式。陈景润发现用“堆垒素数论”第五章的方法可以改进第四章的某些结果。他写了一篇论文 “关于塔内问题” 寄给了华罗庚。华罗庚将陈景润的论文交给中国科学院数学研究所的一些研究人员审查。陈景润的结果被确认是对的。华罗庚认为陈景润是一个很有才能的年轻人。

1956年8月，中国数学会在北京召开 “全国数学论文报告会”。由华罗庚推荐，陈景润应邀参加大会，并报告了他关于塔内 (Tarry) 问题的结果，受到与会者的好评。由于华罗庚的赏识与推荐，陈景润于1957年10月被调到中国科学院数学研究??任实习研究员。

陈景润在中国科学院数学研究所的良好环境中，研究工作进展很快，取得了重要进展。他从研究三角和的估计及其应用入手，对圆内整点问题，除数问题，球内整点问题及华林 (Waring) 问题等著名问题的结果，作出了重要的改进。

从20世纪60年代中开始，陈景润又转入了筛法及其应用的研究，达到了他研究工作的顶峰。他对哥德巴赫 (Goldbach)猜想及殆素数分布的研究成果有广泛的影响，受到国内外数学家的高度评价。

陈景润长期患病，健康欠佳。在 “文化大革命” 中，陈景润受到了错误的批判与不公正的待遇，使他的工作与健康都受到严重的伤害。1984年，陈景润不幸得了帕金森氏综合症，即使在这样的情况，他仍不停地进行研究工作，并常与年轻学生讨论数学问题。1976年，“文化大革命”结束后，陈景润的工作与生活得到了政府很好的照顾，在他病重住医院的几年中，更得到政府对他的特别照顾。1996年3月19日，陈景润因病情加重，治疗无效而去世。

由于陈景润在数学上的突出贡献，他于1977年被提升为中国科学院数学研究所研究员，1981年当选为中国科学院学部委员。陈景润得到过国家自然科学一等奖，何梁何利数学奖与中国数学会华罗庚数学奖。

陈景润于1980年与由昆女士结婚，生有一个儿子。

数学工作

筛法及其应用

1. 表大偶数为素数与殆素数之和

哥德巴赫猜想是1742年哥德巴赫与L. 欧拉 (Euler) 的通信中提出来的关于表整数为素数之和的两个猜想，即

(A) 每一个偶数≥6都是两个奇素数之和;

(B) 每一个奇数≥9都是三个奇素数之和。

显然由 (A) 可以推出 (B)。基于圆法及关于素变数三角和的估计，I.M. 维诺格拉多夫 (Vinogradov，亦译为维诺格拉朵夫) 于1937年天才地证明了：猜想 (B) 对于充分大的奇数成立。因此剩下要证明的就是猜想 (A) 了。利用维诺格拉多夫方法还可以证明，几乎所有的偶数都是两个素数之和。详言之，命E(x) 表示不超过x的偶数中不能表示为两个素数之和的偶数个数。则E(x)=O(x(lnx)^-B)，其中B为任意正常数及与O有关的常数仅依赖于B。

研究猜想 (A) 的另一个方法是筛法。筛法肇源于公元前250年的 “埃拉托色尼 (Eralosthenes) 筛法”。1919年，V. 布伦 (Brun) 对筛法作出了重大改进，并将它用于哥德巴赫猜想。命Pa表示素因子个数不超过a的整数。我们称Pa为一个殆素数。布伦证明了：

(1) 每一个充分大的偶数都是两个素因子个数不超过9的殆素数之和，简单记为 (9，9)。

我们可以类似地定义 (a，b)。不少数学家改进了布伦的方法与他的结果： (7，7) (H. 拉德马赫 (Rademacher)，1924)，(6，6) (T.埃斯特曼 (Estermann)，1932)，(5，5) (A.A. 布赫夕塔布 (Buchstab)，1938，(4，4) (布赫夕塔布，1940) 及(a，b)(a+b≤6)，P. 库恩 (Kuhn)，1954)，其中布赫夕塔布与库恩是将某些组合方法加以巧妙地运用，从而使布伦方法的威力大大地提高了。关于埃拉托色尼筛法的另一重要改进是1947由A.塞尔伯格 (Selberg) 提出来的。综合以上的方法，王元证明了 (3，4)(1956) 与 (2，3)(1957)。

运用布伦筛法，素数分布理论及Yu.V. 林尼克 (Linnik)的大筛法，A.雷尼 (Renyi) 于1948年证明了 (1，c)，即

(2) 每一个大偶数都是一个素数与一个素因子个数不超过c的殆素数之和，其中c是一个常数。

命π(x; k， l) 表示适合p≡l(mod k)， p≤x的素数个数。雷尼关于 (2) 的证明中隐含了下面关于π(x; k，l) 的中值公式：存在δ>0使

(3)

其中(k)表示欧拉函数，

及c₁为常数≥5。1961年与1962年，M.B. 巴尔巴恩 (Barban) 与潘承洞分别独立地证明 (3) 式对于δ=1/6-ε及δ=1/3-ε成立，其中ε为任意正数。而与O有关的常数依赖于ε。潘承洞并由δ=1/3-ε导出 (1，5)。1962年与1963年，潘承洞与巴尔巴恩又独立地证明 (3) 式对于δ=3/8-ε成立并推出 (1，4)。注意有时 (3) 式中的π(x;k，l) 需换成一个加权和。1965年，A.I.维诺格拉多夫 (Vinogradov) 与E.邦别里 (Bombieri) 独立地得出δ=1/2-ε。邦别里的结果得出的k的范围还更大一些，即x1/2/(lnx)^c₂，其中c₂是依赖于c₁的正常数，由此导出了 (1，3)。邦别里-维诺格拉朵夫公式的重要性在于有时可以用它来代替广义黎曼 (Riemann) 猜想。

1966年，陈景润天才地引进了一个转换原理，从而证明了(1，2)，即

(4) 每个大偶数都是一个素数与一个素因子个数不超过2的殆素数之和。命P₁ ，P₂，P₃，P₃表示素数，A=a_v 为一个有限整数集合，及F(A; q， q\') 表示A中适合下面条件的元素个数：

特别记F(A;q\')=F(A; 1，q\').

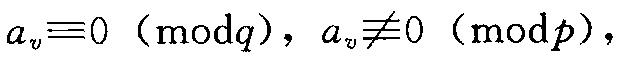
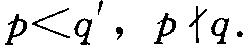
命n为一个偶数，A=n-p，p<n，

及

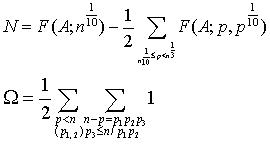
M=N-Ω+O(n^9/10)，

此处(p_1，2)表示条件n^1/10≤p₁<n^1/3≤p₂≤(n/p₁)^1/2。借助于邦别里-维诺格拉朵夫中值公式及各种筛法可以得出N的一个正下界估计，由此即得出 (1，3)。陈景润引进Ω，并给一个上界估计，从而使M有一个正下界。这样就证明了 (1，2)。

2.表偶数为两素数之和的表法数估计

命n为偶数及

表示将n表为两素数之和的表法个数。将塞尔伯格筛法用于集合A=a_v＝v(n-v)，1≤v<n，则可以得到

此处

若将塞尔伯格筛法用于集合A=a_p＝n-p，p<n并用到邦别里-阿·维诺格拉朵夫中值公式，则可以得到

但欲改进系数8，则是很困难的事。1978年，陈景润将系数8改进为7.8342。换言之，他证明了

3. 殆素数的分布问题.

素数论中有一个著名猜想：

(C) 当x≥1时，在区间 [x，x+2x^1/2] 中恒有一个素数。首先是布伦在1919年用他的筛法证明了：当x充分大时，在区间 [x，x+x^1/2] 中存在一个殆素数P₁₁，即猜想 (C) 对P₁₁成立。布伦的结果被不少数学家加以改进。例如王元在1957

年证明了存在 (x>x₀). 我们有兴趣于这样的问题，即对于用殆素数P2代替素数时，猜想 (C) 是否成立?王元于1957年证明了：当x充分大时，有P₂满足

1969年，H.E. 里歇特 (Richert) 将上面的结果进一步改进为

x>x₀.

1975年，陈景润对于P₂证明了猜想 (C)，即当x充分大时有P₂使

(4)

陈景润在证明 (4) 时用到了加权筛法，其中余项估计用到了三角和的估计。1979年，陈景润又用组合方法将 (4) 式中的x^1/2改进为x^0.4777。陈景润的方法成为以后不少重要工作的出发点。

其他工作

4. 华林问题

所谓华林问题是英国数学家华林于1770年提出来的关于表正整数为正整数的等方幂和的问题，即

(D) 对于整数k≥2，恒存在一个仅依赖于k的整数s=s(k)使每一个正整数都可以表示为s个非负整数的k次方幂之和。

这一历史难题是1908年由D.希尔伯特 (Hilbert) 证明的。命使上面结论成立的最小的s为g(k)。问g(k) 等于什么?或其上界估计? 已有的重要结果为g(2)=4 (欧拉，J.L. 拉格朗日(Lagrange) 1770)，g(3)=9很早即被A. 维弗利希 (Wieferrich) 证明。L.E. 迪克森 (Dickson) 与S.S. 皮莱 (Pillai) 独立地证明了当k>6及

(5)

时有d

此处 [x]

表示x的整数部分。皮莱又证明了g(6)=73。于是剩下要处理的只是k=4，5及使 (5) 式不成立的k。陈景润于1964年完全解决了k=5时的情形，即

g(5)=37.

(6)

用陈景润的方法还可以导出g(4)≤20。直至1986年，R.巴拉苏布拉马尼亚姆 (Balasubramaniam)，J.M. 德苏耶 (Deshouillers) 与F. 德雷斯 (Dress) 才证明了g(4)=19。

5. 格子点问题

命r(n) 表示将正整数n分解成两个整数平方之和的分法个数及r(0)=1。则

就等于落在圆u²+υ²≤x中的整点 (μ，υ) 的个数。命d(n) 表示正整数n的因子个数。则

就是在双曲扇形uυ≤x，u≥1，υ≥1中的整点 (u，υ) 的个数。所谓圆内整点问题与除数问题分别为求最小的θ与使对于任何ε>0皆有

A(x)=πx+O(x^θ+ε)

与

D(x)=x(lnx+2γ-1)+O(x^+ε)

成立，此处γ为欧拉常数，而与O有关的常数仅依赖于ε。数论中有一个著名的猜想：

θ=＝1/4

(D)

还有一个著名问题为求黎曼ζ-函数在临界线上的阶，即ζ(1/2+it) 的估计。由于近代处理这些问题的方法都是类似三角和的估计，所以仅叙述圆内整点问题的进展。

首先是C.F. 高斯 (Gauss) 证明了θ=1/2。1903年，G. 沃罗诺伊 (Voronoi) 给予重要改进，他证明了＝1/3。 1906年W.谢尔品斯基 (Sierpinski) 证明了θ=1/3。1923年，J.G. 范德科普 (van der Corput) 引进了某种三角和的估计，将θ改进为θ=^37/112。迄至1942年，最佳结果θ=^13/40是华罗庚得到的。1963年，陈景润将华罗庚的结果改进为θ=12/37，即

(7)

现在最好的估计是H. 依万尼斯 (Iwaniec) 与J. 莫卓溪(Mozzochi)得到的θ=7/22.

类似于圆内整点问题与除数问题的有所谓球内整点问题与虚二次域的类数平均问题。详言之，命B(x) 表示球u²+v²+w²≤x内的整点 (u，v，ω) 的个数。求最小的θ1使对于任何ε>0皆有

这就是球内整点问题。命d为整数>0及h(-d) 表示虚二次域Q(

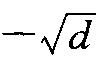) 的类数。类数平均问题就是求最小的₁使对于任何ε>0，

1963年，陈景润与维诺格拉多夫独立地证明了

θ₁＝₁＝2/3

(8)

与圆内整点问题相类似，θ₁与₁也有相应的改进。

6.算术级数中的最小素数问题

命k，l为满足 (k，l)=1的正整数，问在算术级数

kn+l，n=0，1，2，…

中是否有无穷多个素数。这个问题是G.L.狄立克雷 (Dirichlet)于1837年解决的。命P(k，l) 表示上面算术级数中的最小素娄。1934年，S.乔拉 (Chowla) 曾猜想，对于任何ε>0皆有

P(k，l)=O(k1+ε)，

(E)

此处与 “O”有关的常数依赖于ε。首先是林尼克于1944年证明了，存在常数c使

P(k，l)=O(k^c) (9)

潘承洞于1957年最先定出c≤5448。其后不少数学家改进了潘承洞的结果，其中陈景润与他的学生曾证明过C可以取如下之值：

777，168，17，15，13. 5，11. 5.

(10)

目前最佳估计c≤5.5是D.R. 希斯-布朗 (Heath-Brown)得到的。

7. 哥德巴赫数问题

凡可以表示为两个素数之和的偶数称为哥德巴赫数。第1节定义过的E(x) 就是不超过x的非哥德巴赫偶数的个数。1975年，H.L.蒙哥马利 (Montgomery) 与R.C. 沃恩 (Vaughan)将E(x) 的估计改进为：存在δ>0使

E(x)=O(x^1-δ)，

此处与 “O” 有关的常数依赖于δ。1979年，陈景润与潘承洞首次定出

δ>0.01，

(11)

其后陈景润又将δ的估计改进为δ>0.05。

8. 三角和的估计

命q为整数≥2及f(x)=a_kx^k+…+a₁x为整系数k次多项式且满足 (a_k ，…，a₁ ，q)=1。引入完整三角和

其中e(y)=e^2πiy。当f(x)=ax²时，S(ax²，q) 就是有名的高斯和。高斯给出了估计式

(12)

对于一般的完整三角和估计这一著名问题是华罗庚于1940年证明的。实际上，由A. 韦依 (Weil) 的结果可以得出：

(13)

其中c(k)为依赖于k的常数。(13)式右端的阶1^-1/k是臻于至善的。1977年，陈景润给出了c(k) 的估计：

(14)

其中exp(x)=e^x及A (3) =6.1，A (4) =5.5，A (5) =5，A (6)=4.7，A (7) =4.4，A (8)=4.2，A (9) =4.05等。

后记。关于陈景润的生平与工作，过去曾有过一些著作。在撰写本文时，作者参考了这些著作。

简历

1933年5月22日出生于福建省福州市。

1949—1953年就读于厦门大学数学系。

1953—1956年在北京四中，厦门大学工作。

1957—1996年在中国科学院数学研究所工作。

1978年获全国科学大会奖。

1982年获国家自然科学奖一等奖。

1992年获华罗庚奖。

1994年获何梁何利基金科学与技术进步奖。

1996年3月19日在北京逝世。

主要论著

1 陈景润. 华林问题g(5) 的估计. 科学记录，1959，3： 327—330

2 陈景润. 给定区域内的整点问题. 数学学报，1962，12： 408—420

3 陈景润. 圆内整点问题. 数学学报，1963，13： 299—313

4 陈景润. 关于三维除数问题. 数学学报，1964，14： 549—558

5 陈景润. 华林问题g(5)=37. 数学学报，1964，14： 715—734

6 陈景润. 某些三角和的估计. 数学学报，1964，14： 765—768

7 Chen Jingrun. On the least prime in an arithenetical progression. Sci. Sin.，1964，(14)： 1868—1871

8 陈景润. 大偶数表为一个素数及一个不超过两个素数的乘积之和. 科学通报，1966，(17)： 385—386

9 陈景润. 大偶数表为一个素数及一个不超过两个素数的乘积之和. 中国科学，1973，(2)： 111—128

10 陈景润. 华林问题g(4) 的估计. 数学学报，1974，17： 131—142

11 陈景润. 关于区间中的殆素数的分布问题. 中国科学，1976，(1)： 7—20

12 陈景润. 关于算术级数中的最小素数和L函数零点的两个定理. 中国科学，1977，(4)： 383—414

13 陈景润. 1+2系数估计的进一步改进——大偶数表为一个素数及一个不超过两个素数的乘积之和 (Ⅱ). 中国科学，1978，(5)： 477—494

14 Chen Jingrun. On the Goldbach’s Problem and the Sieve methods. Sci.Sin.，1978，21： 701—739

15 Chen Jingrun. On the least Prime in an arithmetical Progression and theorems concerning the zeros of Dirichlet’s L-functions (Ⅱ). Sci.Sin.，1979，22： 859—889

16 陈景润. 关于区间中的殆素数的分布问题 (Ⅱ). 中国科学，1979，(1)： 12—32

17 陈景润，潘承洞. Goldbach数的例外集合. 山东大学学报，1979，(1)： 1—27

18 陈景润，潘承洞. Goldbach数的例外集合. 中国科学，1980，(3)：219—232

19 陈景润. Goldbach数的例外集合 (Ⅱ). 中国科学 (A辑)，1983，(4)： 327—342

20 陈景润. 某种三角和的估计及其应用. 中国科学 (A辑)，1984，(12)： 1096—1103

21 陈景润，黎鉴愚. 关于等幂和问题. 科学通报，1985，30 (4)：316—317

22 陈景润，黎鉴愚. 关于等幂和问题的进一步研究. 科学通报，1985，30 (17)： 1281—1284

23 陈景润. 关于L-函数的零点分布. 中国科学 (A辑)，1986，(7)：673—689

24 陈景润. 关于L-函数的零点分布 (Ⅰ). 曲阜师范大学学报，1986，12 (2)： 1—14

25 陈景润. 关于L-函数的零点分布 (Ⅱ). 曲阜师范大学学报，1986，12 (3)： 1—8

26 陈景润，黎鉴曼. 关于自然数的方幂和. 数学季刊，1987，(1)：1—18

27 陈景润，刘健民. 算术级数中的最小素数和与L-函数零点有关的定理. 科学通报，1988，(10)： 794—795

28 陈景润，王天泽. 奇数情形Goldbach问题研究. 科学通报，1989，34(20)： 1521—1522

29 陈景润，刘健民. 算术级数中的最小素数和与L函数零点有关的定理(Ⅲ). 中国科学 (A辑)，1989，(4)： 337—351

30 陈景润，刘健民. On the least prime in an arithmetical progression(Ⅳ). Sci. Sin. A，1989，32： 792—807

31 陈景润，王天泽. 关于算术级数中素数分布的一个定理. 中国科学(A辑)，1989，(11)： 1121—1132

32 陈景润，王天泽. 关于哥德巴赫问题. 数学学报，1989，32 (5)：702—718

33 陈景润，王天泽. 关于L-函数例外零点的一个定理. 数学学报，1989，32 (6)： 841—858

34 陈景润，刘健民. 关于L函数在直线σ=1附近的零点分布. 科大研究生院学报，1989，6： 1—21

35 陈景润，刘健民. The exceptional Set of Goldbach numbers (Ⅲ). 数学季刊，1989，(4)： 1—15

36 陈景润，王天泽. 关于Dirichlet L-函数的零点分布. 四川大学学报，1990，145—155

37 陈景润，王天泽. Estimation of the second main term in odd Goldbach problem. Acta Math. Sci.，1990，11： 241—250

38 陈景润，王天泽. 关于哥德巴赫问题的一个注记. 数学学报，1994，

34： 143—144

39 陈景润，王天泽. 素变数线性三角和的估计. 数学学报，1994，37：25—31

40 陈景润，王天泽. 关于哥德巴赫问题 (Ⅱ). 数学学报，1996，39：169—174

知名人物 陈景润人物简介

知名人物 陈景润人物简介

·陈景润

知名人物陈景润人物简介

知名人物陈景润人物简介