知名人物 孙永生人物简介
Posted 函数
篇首语：锲而舍之，朽木不折;锲而不舍，金石可镂。本文由小常识网(cha138.com)小编为大家整理，主要介绍了知名人物 孙永生人物简介相关的知识，希望对你有一定的参考价值。
知名人物 孙永生人物简介
·孙永生
孙永生，数学家。长期从事函数逼近论方面的研究，主要成就涉及外尔可微类及其共轭类的最佳逼近问题，切比雪夫最佳逼近，周期函数类上线性算子的逼近以及兰道不等式和逼近论中的宽度问题等。
孙永生，1929年1月22日生于河北省沧县望海寺村。1947年高中毕业后，入北平师范学院 (现北京师范大学) 数学系。1948年从北平赴华北解放区正定县，在华北大学第二部政治班学习并加入中国新民主主义青年团。结业后分配到华北大学工学院学习。1949年10月回到北京师范大学数学系。1952年毕业于北京师范大学，同年加入中国共产党。1954年赴苏联学习。1958年毕业于莫斯科大学，获数学-物理副博士学位。其后一直在北京师范大学任教。从1965年到1982年担任数学系副主任，1983～1993年担任该系学术委员会主任。1990～1994年任国家教委首届高等学校数学力学教学指导委员会委员。他还是科学出版社《现代数学丛书》和北京师范大学 《现代数学丛书》 编委，以及我国主办的国际学术期刊 “Approximation Theory and Its Applications”、俄罗斯和保加利亚主办的国际学术期刊 “East Journal on Approximations”、《数学季刊》、《数学研究》 的编辑委员。
孙永生在逼近论方向的研究成果和陆善镇在实哈代 (Hardy) 空间方向的研究成果获得了1988年国家教委科技进步一等奖和1989年国家第四届自然科学四等奖。他的专著 《函数逼近论》 (上、下册) 为我国函数逼近论专业方向研究生广泛使用，在1992年获国家教委颁发的高校出版社优秀学术著作特等奖。他共培养了14名博士，18名硕士，另外还有34名访问学者和进修教师。这当中已有9人晋升为教授，4人被批准为博士生导师。他和陆善镇获得了1993年北京市高等学校优秀教学成果二等奖。他是新中国自己培养成长的第一代数学工作者，是函数逼近论方向有成就的数学家和学术带头人之一。
勤奋好学，知难而进
孙永生祖父是个中医，家里有田产，在当地是富裕户。伯父孙震涛在20年代毕业于北平师范大学化学系，毕业后做中学教师。父亲孙震营读过几年小学，在农村生活。孙永生七八岁时在村里念过1年小学，1年私塾。1937年 “七七” 事变后随父母离乡。1940～1941年在沧县县城住了1年，毕业于县立牛市街小学，后考入沧县师范初中部。那时沧县已经沦陷，日本侵略军对学校控制很严，条件极差。1941年以后父母又搬回乡下，他在校住宿，生活很艰苦，伙食极差，学生经常吃不饱。孙永生埋头读书。那时他对数学产生了浓厚兴趣，对课堂上讲的不能满足，就利用课余时间来自学。3年内不但超前学完了全部初中数学，而且自学了部分高中数学科目，读了金品、叔桂超合编的 《几何学》，严济慈的 《几何证题法》，做了大量几何难题。1944年考入北平市立高中。孙永生利用该校较好的师资和设备条件，更加埋头念书。他的学业在班上经常名列前茅，尤对数学情有独钟。高一时期热衷于初等平面几何，自学过王邦珍、R. 约翰逊(Johnson) 等人的初等近世几何的著作。高二以后，兴趣转移到代数和解析几何。除了范氏代数外，他自学过林鹤一、L.E. 迪克森 (Dickson) 的初等方程式论的书。他在高中不但养成了自学习惯，而且也形成了自己的一套自学方法。高中毕业后，他被学校保送进了北平师范学院数学系。大学一年级的课程除了微积分、立体解析几何、初等方程式论等数学科目，还有大量非专业课程，一周的学时高达40节课。他对那些枯燥无味的课程一律采取应付态度，集中精力自学了竹内端三的 《极限论》，R. 戴德金 (Dedekind) 的《Irrational Number and Continuity》。
那时候国民党政治腐败，崩溃之势已见端倪。学校中社团很多，学生运动如火如荼。孙永生埋头读书，从不参加社团活动。但是他有正义感，对国民党政权的腐朽深为不满，对其疯狂压制学生的爱国民主运动的种种暴行深恶痛绝。大学读书环境的日趋恶劣使他深感不安。到了1947年底，他对所处的环境越来越感到厌恶。经过和高中时期的同学王鸿书、许忠 (时在唐山工学院) 反复密商，终于下决心于1948年3月23日结伴离校奔赴华北解放区。是年4月到达正定县，进了华北大学第二部政治班第十二班学习，接受初步的革命人生观教育。1948年8月政治班结业后，他和十几位同班学友被分配到设在井径的华北大学工学院学习业务。华大工学院是华北解放区培养工程技术人员的最高学府。工学院领导热情欢迎这十几位新学员，特别批准孙永生、李讲、吴沙凡三个人学习数学. 为此，成立了一个数学自修组，自学微积分和微分方程。到1948年12月中旬，华北人民政府从华大工学院抽调数十名学员奔赴平津前线，准备于平津解放后参加接管国民党的工矿企业。孙永生参加了这项工作。他随大队于12月底到达北平市郊，俟北平解放后参加了接管华北钢铁公司的工作。接管工作结束后，于1948年5月又回到井径。1949年8月，华大工学院迁到北平，孙永生返回北京师范大学数学系，从一年级重读。解放后的北京师范大学数学系由傅种孙任系主任。孙永生仅仅读了3年，在1952年8月提前一年毕业。在这3年里政治运动很频繁，孙永生是青年团干部，社会工作重，课外活动很多。他不满足于课堂上安排的那几门基础课，很想利用课余时间多念点书，但苦于时间太少，仅仅自学了熊庆来的 《高等算学分析》 和哈代的 《Pure Mathematics》 等分析类的著作。到毕业时，他对微分方程、概率论、拓扑学、泛函分析、函数论几乎一无所知。所幸的是，他从中学时期就养成了自学习惯，形成了自己的一套自修方法; 培养了一种锲而不舍、知难而进的勤奋好学的精神状态。
毕业后，孙永生被分配到北京俄文专修学校留苏预备部做了一个学期的文化教员。1953年1月孙永生被调回北京师范大学数学系，协助张禾瑞举办 “师范师专算术代数课讲习班”。孙永生突击翻译了苏联教材 《算术》、《代数和初等函数》作为讲习班教材。借此机会他自学了张禾瑞的 《近世代数基础》 和施伯纳 (樊畿译) 的 《解析几何与代数》。1953年7月系里推荐孙永生和袁兆鼎参加留苏预备考试。他们得到录取，遂于1953年10月到俄专留苏预备部。经过10个月的准备，到1954年9月踏上赴莫斯科的旅途。
留学苏联，专攻函数逼近论
1954年9月大批留苏预备生到达莫斯科。准备学数学的研究生有周毓麟、张芷芬、陈庆益、袁兆鼎、孙永生和董明德 (力学) 6人。他们都被分配到莫斯科大学力学数学系。孙永生的指导教师是一位函数逼近论的青年专家S. 斯切契金 (Stechkin)教授。斯切契金教授为孙选定了专业方向： 实函数逼近论，制订了一个一年半的学位课程计划。首先要补上常微分方程论和数学物理方程两门大学课程。学位课程则包括函数论 (实变与复变)、泛函分析、三角级数论、函数逼近论以及发散级数求和理论。
1955年秋季孙永生参加了斯捷克洛夫 (Steklov) 研究所为其硕士生组织的 “拓扑学和泛函分析”讨论班。他在莫斯科大学选听了著名学者D. 闵绍夫 (Menshov) 教授主讲的发散级数求和及N. 巴里 (Bari) 教授主讲的三角级数论，经常参加由闵绍夫、巴里主持的函数论讨论班。这个讨论班在莫斯科大学力学数学系举行，每周1次，吸引了莫斯科市的许多函数论方向的专家学者。这些课程和学术活动，不但引导他进入了现代函数论的重要领域，而且莫斯科大学浓厚的学术氛围，俄罗斯分析学派的严谨、创新、精细的学术风格，巴里、闵绍夫等一批当代数学大师的学者风范和人格魅力，使孙永生为之倾倒，其印象终生难忘。
1956年1月我国学者曾远荣、徐利治两位教授去莫斯科大学，参加在那里举行的国际泛函分析讨论会。孙永生在会上结识了徐利治，帮助徐利治和斯切契金建立了联系。是年6月我国派了??个庞大的代表团赴莫斯科参加全苏第3届数学大会，会场就设在莫斯科大学力学数学系。孙永生等也参加了大会。他在这里结识了陈建功、程民德两位教授，帮助他们和苏联同行建立联系。
1956年上半年斯切契金在讨论班上提出了几个问题，鼓励孙永生去作。他的指导相当具体，不但提出问题、介绍问题的背景和有关文献，而且阐述自己对解决问题的一些思路，并预测可能的结果。这对刚想跨进科研门槛的研究生非常宝贵，可以引导他们较快地进入工作状态。不过，孙永生在开始阶段工作并不顺利。到1956年底，他证得了一些结果，但主要是模仿、推广，没有体现出创造性。孙永生自己对此颇为苦恼。1957年初，他读了V. 贾岱克 (Dzjadyk) 1953年发表的一个工作，解决了当0<r<1时周期的外尔 (Weyl) 可微类
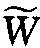∞T用n阶三角多项式的最佳逼近常数的精确计算问题。这个结果为完全解决法国数学家J.法瓦尔 (Favard) 在1936年提出的外尔可微类及其共轭类的最佳逼近常数精确估计问题迈出了重要一步，因而在当时苏联函数逼近论学者中间颇受重视。 但是， 到1957年， 对于
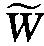∞r的共轭类，以及r>1的情形，问题都有待解决。由于r>0时，若r不是整数，函数类及其共轭类的卷积核没有了对称性，因此对它验证马尔可夫 (Markov) 准则变得十分困难。孙永生本打算解决r>1情形，但是花费了半年时间，克服了很多困难，仅仅得到了部分结果 (r>6)。但斯切契金对这项结果很满意。孙永生的副博士学位论文经S. 尼科尔斯基 (Nikolskii)、贾岱克两位教授的审查，颇受赞赏，于1958年2月顺利通过了答辩，得到了物理-数学副博士学位。建立研究梯队，学术成果累累
1958年3月孙永生返回到北京师范大学，他希望尽快地组织起实变函数论讨论班，把研究工作继续下去。1958～1960年间政治运动频繁，这是办不到的。1961年秋季学校恢复了正常教学秩序，一些受到冲击的基础学科的教学科研开始恢复。陆善镇从华东师范大学数学系毕业后分配到北京师范大学，他们两人商定成立一个实变讨论班。1962年初实变讨论班运转起来了，总共有3个成员 (包括张阳春)。他们选择了三角傅里叶分析和实变逼近论做为研究方向。孙永生继续研究外尔类的三角逼近问题，陆善镇则专攻多元傅里叶分析。这个讨论班存在了3年半，到1964年10月因 “四清运动” 而停顿。经过 “文化大革命”，直到1978年年底讨论班才恢复。到现在，这个当年仅有3个成员的讨论班，已经发展成拥有7位教授的具有较高素质的研究梯队，在3个研究方向上卓有成效地开展着工作。陆善镇、丁勇、杨大春3位教授主持着哈尔-赫茨 (Herz) 空间和考尔德伦-济格蒙德 (CalderonZyd) 算子论方向; 孙永生、房艮孙、刘永平3位教授主持着逼近论的极值问题和信息复杂性理论方向; 王昆杨、刘永平两位教授主持着多元逼近、球面调和分析和特殊函数的交叉问题方向。这些方向和当前国际上的主流学派息息相通，密切接轨。经过了20年的工作，有了较深厚的学术积累，做出了在国内外有影响的工作。
1958年以来，孙永生在函数逼近论方向发表学术论文 (包括与他人合作的) 达70多篇，出版专著一部，其他著作 (教科书，译著) 7种。下面扼要介绍孙永生和他的学生们的一部分主要工作。
1. 切比晓夫最佳逼近
1958～1962年间，孙永生完全解决了在外尔意义下的可微周期函数类 (即是具有非整数阶有界导数的周期函数) 及其共轭类借助于次数不超过n的三角多项式子空间所最佳一致逼近的逼近常数的精确估计问题。微分指标r>1时得到了基本函数类及其共轭类上的精确解，而1/2≤r<1时共轭情形的结果比贾岱克的工作早12年发表。这项结果得到了国际同行的高度评价。苏联函数逼近论著名学者N. 克涅楚克 (Korneichuk) 院士于1974年在苏联科学院斯切克洛夫数学研究所的一次学术报告中称赞这一结果 “是对逼近论的极值理论的重要贡献”。A. 济曼 (Jiman)，克涅楚克以及V. 吉哈米洛夫 (Tikhominov) 等国际著名的逼近论学者在他们的关于函数逼近论著作中多次引述这一结果。
2. 周期函数类上线性算子的逼近
1979～1980年间，孙永生研究正阶切萨罗 (Cesaro) 平均对周期连续函数和周期可积函数分别在一致尺度及L1尺度下的逼近误差，得到了该误差的杰克森 (Jackson) 不等式的最佳常数的强渐近估计，证明了在两种尺度下的杰克森逼近常数具有相同的渐近展开的主项。
在这期间，孙永生还研究了具有正核的多项式型周期卷积算子的逼近性能，得到了很广泛的结果。他引入了一类称为弱正核的卷积算子以代替正的多项式核，并且对弱正型算子在周期的索伯列夫 (Sobolev) 类上的整体逼近建立了广泛的结果。这项成果包含了从20世纪40年代以来苏联学派的逼近论学者尼科尔斯基，斯切契金等人在这一方向给出的一些具体结果，而且本质地改进了M. 马托尼 (Motornii)发表在1974年的工作。至今这仍是关于该问题的最好结果。
以上两项结果都发表在 《数学学报》上。
3. 兰道 (Landau) 不等式
斯切契金在20世纪70年代初发现经典的兰道不等式的精确常数问题和逼近论的几个重要极值问题的精确解间的一个深刻联系，引起了人们对该问题的兴趣。孙永生在1984年把兰道-柯尔莫戈洛夫 (Kolmogorov) 不等式拓广到由任意常系数的线性微分算子确定的索伯列夫类上，他的结果包含了70年代以来国际上发表的几个著名结果 (美国的S. 卡林 (Karlin)，1976; 加拿大的沙尔玛 (Sharma) 和齐巴拉力奥 (Tzimbalario)，1977; 荷兰的特·莫舍 (Ter Morsche)，1985)。孙永生利用该结果完整地解决了微分算子D在由一个仅仅具有实特征根的线性微分算子确定的索伯列夫类上的最优回复问题。该问题系由美国数学家C. 米切里 (Micchelli) 在1977年提出，他得到了部分解。
4. 宽度
逼近论中宽度问题的研究肇端于柯尔莫戈洛夫发表于1936年的开创性工作。但是在这以后直到20世纪50年代末，这一问题的研究基本上处于停滞状态。20世纪60至70年代经过吉哈米洛夫，K. 巴边科 (Babenko)，克涅楚克，米切里，A. 平库斯 (Pinkus) 等国际上著名逼近论学者的大力工作而成了逼近论发展的一个热点，以其问题的艰深，和现代数学的许多分支的广泛联系而吸引了国际上许多数学家的注意。孙永生在1980至1982年间注意到这一方向。他奋力拼搏，阅读、整理了大量文献，吸收了该方向的最新成果，接近了国际前沿。1983年，他发表了自共轭常系数线性微分算子的格林 (Green) 函数关于指标 (∞，p) 的柯尔莫戈洛夫n宽度的精确估计及极子空间构造的结果 ( 《中国科学》，A辑，1983，第8期)，这个结果回答了米切里和A. 梅尔克曼 (Melkman) 在1977年提出的关于全正核宽度的一个猜想。在1983～1985年间孙永生和黄达人合作继续这一方向的研究，在由常系数线性微分算子确定的周期索伯列夫类上的宽度和单边宽度的精确估计问题的研究中得到了系统的结果。其中一部分主要结果发表在 《逼近论及其应用》 (ATA)，?科学通报》 等期刊上，并且曾在1983年美国A&M大学举行的国际第四届逼近论大会上，以及1985年在杭州举行的中美逼近论联合讨论会上做过报告。
5. 平均宽度和最优插值
从1985年起，孙永生把注意力集中到研究定义在全实轴上的光滑函数类的最优恢复问题。 他首先提出了利用基数是
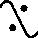0aleph的线性信息族对上述函数类的最优插值的研究。这一课题把最优恢复问题从利用有限基数的线性信息族对以紧集为定义域的、紧致的函数集为回复对象的情况实质性地推进了一步。1985～1989年期间，他连续发表了 “全实轴上的可微函数类上的最优插值(Ⅰ)” (ATA，1985)、“全实轴上可微函数类的最优恢复” (科学通报，1986. 11) 等3篇论文，把对一致范数情形的研究逐步展开并引向深入; 稍后和李淳合作研究L2范数情形，完全解决了索伯列夫类W21(
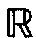) 在L2 (
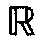) 内借助于可数个线性信息的最优回复问题。1989年9月，苏联著名的函数逼近论学者吉哈米洛夫和克涅楚克来我国访问。 吉哈米洛夫介绍了他对
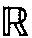上的索伯列夫类的宽度问题的一些思考，特别介绍了他基于香农(Shannon)-柯尔莫戈洛夫熵的思想提出的关于无限维线性子空间的平均维数的概念，他以此为基础建立了全实轴上的索伯列夫类的平均宽度概念。吉哈米洛夫了解到他的工作和自己的想法关系十分密切，对他的工作极感兴趣。通过和俄罗斯学派的交流，孙永生把自己的想法和吉哈米洛夫的想法结合起来，带领博士生展开了深入系统的工作。1989～1993年间，在他和黄达人、房艮孙等得到了一些基本结果的基础上，他的博士生陈迪荣、刘永平、房艮孙等得到了一系列进一步的深刻结果，不但完全解决了
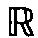上索伯列夫类WpT(
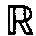) 内的平均柯尔莫戈洛夫宽度和最优插值的精确解，而且更进一步地引入了一个新的函数类： 索伯列夫-维纳 (Weiner) 类WpqT (
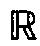)， 在p≥q≥1条件下圆满解决了WpqT(
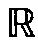) 在Lq (
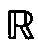) 内的平均宽度和最优差值问题， 从而建立起了在
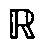上和T上完全类似的结果。 这一轮工作成果十分丰硕，和俄罗斯吉哈米洛夫学派的工作并驾齐驱，互有交叉，其中对索伯列夫-维纳类的研究，以及对全实轴上以PF密度为核的卷积类的研究，是孙永生和他的学生们的独特的工作。此外，陈迪荣在其博士论文中部分地证实了平库斯关于B核宽度的第二猜想。至今，这仍是在该问题研究中的最好结果。孙永生和他的学生们的这一轮工作得到了国际国内同行的重视和好评。吉哈米洛夫教授于1991年致函孙永生，信中写道：“您和我以及我们的学生们几乎同时提出了旨在实现全实轴上逼近的广泛计划，这给我留下了非常深刻的印象。” 他在1995年俄刊Mathematical Survey上发表文章，其中提到 “孙永生的学术集体独立于我们，提出了与我们的想法相近的思想。他们是通过研究全实轴上的最优插值问题实现其想法的。” 德国埃尔兰根大学H. 贝伦斯 (Berens) 教授在评价陈迪荣的博士论文时写道：“在逼近论中宽度问题被认为是难度最大的一个领域……在中国，孙永生教授是这一方向研究中起带头作用的分析学家，他和他的学生们作了出色的工作，特别是在宽度和最优恢复的结合方面。”
徐利治教授指出 (《数学研究与评论》，1991，11 (4))： “以孙永生为代表的北京师范大学逼近论研究集体，多年来努力继承和发展前苏联函数构造论学派的传统优势之后，确实已经在中国结出丰硕成果，并引起国际同行的注意……孙永生、黄达人与房艮所建立的某些周期卷积类上宽度估计的精确结果，大大拓广了前苏联学派和平库斯等外国学者的工作，确实具有深刻的理论意义和价值。”
6. 最近几年，孙永生把研究注意力转到多元问题，特别关注逼近论与数值分析和连续问题的信息复杂性问题的交插，他和他的学生汪成咏、汪和平、蒋燕杰、罗俊波等人在多元最优公式，线性算子方程的近似解法及其复杂性，在带概率测度的巴拿赫 (Banach) 空间内的宽度和随机逼近等广泛的方向取得了??批新结果。
孙永生在逼近论方向的研究成果和陆善镇在实哈代空间方向的研究成果获得了1988年国家教委科技进步一等奖和1989年国家第四届自然科学四等奖。他的专著《函数逼近论》 (上、下册)为我国函数逼近论专业方向研究生广泛使用。
“学为人师，行为世范”
北京师范大学的校训是 “学为人师，行为世范”。对此，孙永生教授始终身体力行。他不仅是一位卓有成就的科学家，也是一位优秀的教育工作者，一个高尚的人。20世纪80年代，孙永生已年近花甲，在担负繁重的科研工作和行政工作的同时，仍然兢兢业业做本科生的教学工作。那些年，尽管没有课时津贴，他却年年超工作量，其数额总在全系名列前茅： 1984～1985学年超额983学时，居全系之首。在多年的教学实践中，孙永生的课堂教学，已经讲出了自己独特的风格： 系统完整、深入浅出、??丝不苟、富有启发。许多学生谈起从孙永生教授讲的课中得到的教益，总是感慨和称赞不已，认为听孙永生教授的课，不仅学到宝贵的知识，而且可以学到高超优美的讲课艺术，是一种高境界的精神享受。
孙永生对学生热忱负责。有的学生不懂俄文，他就亲手把俄文文献翻译成中文发给学生。经他手译给学生的稿子，不只??篇，有的还相当长。他的精神具有巨大的无言的感染力和号召力，使他的学生们在感动和钦佩之余，不敢有丝毫懈怠。当他领导自己一手组织培养的学术研究集体取得了重要成果时，孙永生总是把功劳归于集体，使得这个集体获得国家的奖励，从而把奖励化为集体前进的动力。他的学生们切身体会到自己的老师是多么热切、多么真诚地把希望寄托在年轻人身上。孙永生对研究生从录取到培养要求都非常严格。当年，有一位研究生考生，平时业务成绩较好，但在研究生考试中没有合格，孙永生坚持原则，没有录取。有一位硕士生，学习有困难，不能合格地完成学业，孙永生规劝他不要勉强，这位学生充分理解了先生，自动放弃了学位要求，以积极奋进的态度走上了自己生活道路上的新历程。孙永生为人正派，品德高尚，工作勤奋，谦虚谨慎，事事以身作则，严格要求自己，热情关心他人。当同事遇到困难的时候，他总是伸出热情的援助之手; 在荣誉和利益面前，他总是谦让其他同志。他的崇高的精神境界是人们学习的榜样。他在全系党员和群众中也享有很高的声誉。1986年数学系党总支评选他为优??共产党员。在退休前夕，孙永生得了肺癌，做了手术。面对疾病，他表现了一个唯物主义者的大无畏气概。手术之后，他和同样患有癌症的夫人一道坚持锻炼身体。当健康状况得到恢复后，他仍然继续参加力所能及的学术研究活动，热情地关怀着函数逼近论小组的学术研究工作和教学工作，除了提出指导性的建议外，经常参加讨论班，和大家一起研讨。当俄罗斯学者和乌克兰学者来访问时，他都来参加报告会和讨论会，义务给大家当翻译。
孙永生于1999年4月退休。1999年5月8日北京师范大学数学系为了庆贺王世强、孙永生、严士健、王梓坤、刘绍学5位教授执教50年举行了隆重的庆祝会。孙永生在致答词时说： “我就要成为科教战线上一个退役的老兵了，但我并不感到孤独，因为有我们的学术集体在。我仍然是你们中间的一员。”
简 历
1929年1月22日 出生于河北省沧县望海寺村。
1952年 毕业于北京师范大学数学系。
1958年 毕业于前苏联莫斯科大学力学数学系研究生部获数学-物理学副博士学位。
1958年 任教于北京师范大学数学系，1961年晋升副教授，1979年晋升教授，1981年为博士生导师。
1965—1982年 任北京师范大学数学系副主任。
1983—1993年 任北京师范大学数学系学术委员会主任。
1987—1992年 任北京师范大学学位委员会委员。
1990 — 1995年 任国家教委首届高等学校数学力学教学指导委员会委员。
主要论著
1 Sun Yongsheng.Best approximation of classes of functions representable in convolution form (in Russian) .Dokl.Akad.Nauk USSR，1958，118(2)： 247—250
2 Sun Yongsheng，Best qpproximation of periodic differentiable functions by trigonometric polynomials (In Russian) .Izv.Akad.Nauk USSR Math.Series，1959，23 (1)： 67—92： 1961，25： 143—152
3 孙永生. 用三角多项式近迫周期可微函数. 数学学报，1962，12 (3)：181—202
4 孙永生. 周旋函数的最佳一致近迫和最佳线性近迫. 数学学报，1962，12 (3)： 301—319
5 孙永生 (与张阳春合作). 一对共轭周期函数的最佳逼近的渐近性质。数学学报，1964，14 (4)： 578—596
6 孙永生. 实变函数逼近的几个问题，《全国第一届函数逼近论会议论文集》. 杭州： 杭州大学出版社，1979，25—43
7 孙永生. 关于Cesaro算子的逼近常数. 数学学报，1981，24 (4)：516—537
8 孙永生. 周期函数利用线性算子的L1平均逼近. 数学学报，1982，25(3)： 561—577
9 孙永生. 广义完全样条类上的最小范数问题以及与之有关的宽度问题.中国科学 (A辑)，1983，(8)： 677—688
10 孙永生. 光滑函数类的宽度估计问题，《全国第一届函数逼近论会议论文集》. 南京： 南京大学出版社，1983
11 孙永生. 关于周期可微函数类上的某些极值定理. 北京师范大学学报(自然科学版)，1984，20 (4)： 11—26
12 SunYongsheng (with Huang Daren).One-sided approximation of Ωp2r+σ.ATA(逼近论及其应用)，1984，1 (1)： 19—35
13 孙永生. 关于线性微分算子的Landau-Kolmogorov不等式. 科学通报，1985，7： 481—484
14 孙永生 (与黄达人合作). 广义Bernoull核的宽度. 科学通报，1985，12： 728—731
15 Sun Yongsheng.Optimal interpolation for a differentiable function class(Ⅰ) .ATA，1986，2 (4)： 49—54
16 孙永生. 可微函数类的最优回复. 科学通报，1986，11： 809—812
17 Sun Yongsheng.Optimal interpolation on some classes of differentiable function on R，《国际第五届逼近论会议》，1986年1月，Texas AdM大学，Acad.Press，1987，583
18 孙永生. 一个卷积类上的最优插值问题. 科学通报，1988，13：464—467
19 孙永生. 函数逼近论 [上、下册 (下册与房艮孙合作)]. 北京： 北京师范大学出版社，1989; 1990
20 Sun Yongsheng.Optimal; recovery of the derivative from a class of smooth functions，《国际第六届函数逼近论会议》，1989年1月，美国Texas AdM大学，Acad.Press，1990
21 SunYongsheng (with Li Chun) . Best approximation of differentiable functions by cardinal-splines of higher order (In Russian) . Matem Zameki(Math. Notices)，1990，10
22 Sun Yongsheng (with Li Chun) . Optimal recovery of W2T(R) in L2(R). Acta Math. Sinica (New Series)，1991，7 (4)
23 Sun Yongsheng (with Chen Dirong) . Hardy-Littlewood-Polya inequality for a linear differential operator and some related optimal problems. ATA，1992，8 (1)： 50—58
24 Sun Yongsheng. Average n-width of point sets in Hilbert space. Chinese Sci. Bulletin，1992，37： 14
25 Sun Yongsheng (with Liu Yongping) . Optimal recovery of the SobolevWeiner class of smooth functions by double sampling. Constructive Approximation，1993，9： 391—405
26 Sun Yongsheng (with Wang Chengyong) .μ-Acerage n-widths on the Wiener space. J. Complexity，1994，10： 428—436
27 Sun Yongsheng (with Wang Chengyong) . Average error bounds of best qpproximation of continuous functions on the Weiner space.J. Complexity，1995，11： 74—104
28 Sun Yongsheng (with Wang Chengyong)，Average error bounds of best approximation in a Banach space with a Gaussian mearure. East J. on Approx.，1995，1 (4)： 431—439
29 Sun Yongsheng (with Wang Heping) . Representation and approximation of multivariate periodic functions with a bounded mixed modulous of smoothness. Proc. of Steklov Math. Ins. V. 1998，219： 350—371
30 孙永生. 各向光滑性不同的多元函数类的作优恢复和宽度. 数学进展，1998，27 (1)： 69—77
31 Sun Yongsheng (with Liu Yongping，Chen Dirong) .Extremal problems in approximation theory for some classes of smooth functions defined on Rd. 北京师范大学学报 (自然科学版) (增刊)，1999，35： 79—144
32 Sun Yongsheng.Optimal subspaces for a peroodic convolution class with a B-kernel.East J.on Approx.，2000，6 (1)： 53—63
相关参考
刘永生刘永生是优秀的无产阶级革命战士。他从1928年参加永定暴动起，在福建、广东、江西三省边界地区坚持敌后游击战争20多年，为人民的解放事业进行了艰苦卓绝的斗争。新中国成立后，他先后担任10兵团副司令
在俄罗斯国内，以及美国、欧洲许多国家，一个神秘的传说已经被越来越多人相信并传播，那就是：>俄罗斯是的，他是一个传说中的不人，，他不停的变换身份和地点，掩盖自己的秘密。带你解密：>1.也译作、，外网上一
历史人物 凄美彼岸花的传说，冥界唯一的花(永生永世不能相见)
本站网：小编整理了一些关于“凄美彼岸花的传说，冥界唯一的花(永生永世不能相见)”的详细内容,方便你详细了解！彼岸花开在黄泉路上，是冥界唯一的花，死人花带有一丝悲伤的意味。彼岸花的传说也非常的凄美，两人
永生
来源：脑洞历史观话说晚清末年，慈禧老太后突然脑洞大开，发动群众，也就是义和团对付洋人，一时间杀洋人，掀教堂，搞得不亦乐乎。等于向全世界宣战。这说明，女人的胆子要是大起来，丫的根本拦不住啊。洋人一吃亏，
三国人物本名：关羽字号：云长，永生所处时期：东汉民族族群：汉人出生地：河东解良作古时候：220年重要造诣：白马斩颜良，襄樊败于禁职业：将领官职：前将军爵位：汉寿亭侯谥号：壮缪侯（历史lishixinz
历史人物 孙元化的主要事迹 孙元化的人物生平 孙元化的人物简介
本名：孙元化 别称：孙初阳，孙火东 所处时代：明朝www.cha138.com 民族族群：汉族 主要作品：经武主编孙元化——明朝西洋火炮专家 孙元化为一代儒将，其祖父孙抬是明给事中孙浚的
历史人物 孙传芳简介 孙传芳是怎么死的 孙传芳盗墓 孙传芳子女
中文名：孙传芳 别名：孙馨远 国籍：中国 民族：汉族 出生地：山东省泰安市 出生日期：1885年4月17日 逝世日期：1935年11月13日www.cha138.com 职业：直系军
林永升林永生字钟卿，出生于福建福州，曾入学福州船政后学堂，曾在英国皇家海军学院学习深造，之后成为经远舰的管带。甲午海战中，经远舰被日舰击沉，林永升中弹破脑而亡，清政府追赠他为太子少保。林永升简介>林永
历史人物 孙贵妃的主要事迹 孙贵妃的人物生平 孙贵妃的人物简介
所处时代：明朝 民族族群：汉 出生时间：1344年www.cha138.com 去世时间：1375年 封号：贵妃 谥号：成穆孙贵妃——明太祖朱元璋宠妃 元末兵乱，孙氏父母俱亡，跟随仲兄