知名人物 周学光人物简介
Posted 知
篇首语：我们这个世界，从不会给一个伤心的落伍者颁发奖牌。本文由小常识网(cha138.com)小编为大家整理，主要介绍了知名人物 周学光人物简介相关的知识，希望对你有一定的参考价值。
知名人物 周学光人物简介
·周学光
周学光，数学家。主攻代数拓扑学，主要成就涉及同伦论，特别是 (n-1) 连通的n+r维多面体的伦型以及球面同伦群等领域。
周学光1927年6月5日出生于四川省资中县。早年在中学数学老师胡鹏先生的影响下，对数学产生浓厚兴趣，后考入成都市四川大学数学系并于1948年以优异成绩毕业，并留校任教。在大学就读期间，在杨宗磐教授 (已故，当时执教点集拓扑学)的影响下，开始涉足代数拓扑学的学习和研究。在四川大学任教两年后于1950年前往天津市南开大学数学系任教。在这期间，凭着执著的追求和顽强的毅力，主要通过自学，深入掌握了当时代数拓扑学的基础知识和国外研究文献的内容，开始了毕生的代数拓扑学研究生涯。
1950年至今，周学光在南开大学数学系先后任助教，讲师，副教授，教授，博士生导师，副系主任，系主任，中国数学会天津市分会副理事长，理事长等职，在做好教学工作和社会工作的同时，毕生从事代数拓扑学的研究工作，主要是同伦论及其应用。从1956年发表第一篇论文起，至今共发表同伦论的研究论文30余篇，取得了许多在国内外有广泛影响的重要成果，在同行专家中享有很高声誉，是我国同伦论研究的奠基人之一。
在20世纪50年代，周学光解决了 (n-1) 连通空间的(n+2) 维同伦群的确定问题和 (n+2) 维多面体到 (n-1) 连通空间的映射的同伦分类问题; 这是1953年国际拓扑学会议上提出的两个问题，因此获得国内外学者的高度评价。1958年，周学光在《数学学报》，《中国科学》发表论文，指出了日本拓扑学家Shiraiwa提出的关于 (n+3) 维 (n-1) 连通多面体的伦型的著名定理的错误，又指出应如何改正，并在这基础上建立了能确定空间伦型的特征上同调运算。这一工作统一了著名的前苏联拓扑学家M. M. 波斯尼科夫 (Postnikov) 和英国拓扑学家J. H. C. 怀特黑德 (Whitehead) 关于伦型问题的理论，在当时国际代数拓扑界中获得公认并引起广泛而强烈的反响。由此周学光在国内外代数拓扑界享有很高声誉。
在60年代，周学光在原来工作的基础上建立和发展了特征上同调运算理论，另外又给出了无限多个上同调运算的一组基底，证明了任意一个上同调运算都可以用这组基底惟一地表示出来，大大简化了无限的上同调运算之间的关系，丰富和发展了上同调运算的理论。
进入80年代以来，周学光加强了同国外拓扑学家的学术交流，先后数次赴美国参加代数拓扑学国际会议和学术年会。他用切割法建立了差不多闭的流形在欧氏空间中嵌入的新理论，概括和统一了前人在这方面的结果。在斯廷罗德 (Steenrod) 代数的上同调方面，他建立了一个有序链复形的计算方法。使庞杂的计算变得有规律可循并予以简化，被国外拓扑学家评论为首创。利用这种方法，在球面同伦群计算这一世界公认的难题中，周学光证明了β元素和科恩-格尔斯 (Cohen-Goerss) 元素的户田 (Toda) 乘积不等于零，由此得出球面稳定同伦群的无穷多族新元素，大大丰富了对球面同伦群的认识。
自80年代初我国建立自然科学基金制以来，周学光先后连续主持了国家自然科学基金，国家教委博士点基金和国家数学天元基金等研究项目，其研究成果于1985年获国家教委优秀成果奖和1991年国家教委科技进步奖。他先后培养硕士和博士研究生20余名，为同伦论研究培养了一批骨干。在他的带领下，南开大学数学系形成了一个拓扑学研究集体，近10年来已发表数十篇高水平的论文。
我国同伦论研究的一位奠基人
20世纪初H. 庞加莱 (Poincaré) 创立组合拓扑学之后，在20年代，抽象代数中群论的方法得到普遍的运用，组合拓扑学变成了代数拓扑学，其中关于同调群这类空间的拓扑不变量的认识已趋成熟。继代数拓扑学的同调论这一分支形成之后，在30年代，以W. 胡雷维奇 (Hurewicz) 为标志，开始研究空间的同伦群这类更具活力的拓扑不变量。简言之，空间X的n维同伦群是n维球面Sn到空间X的连续映射按同伦关系进行分类而得的同伦类集合，它可给予群结构而成为同伦群πn(X)。大约在1935年，胡雷维奇证明了对 (n-1) 连统空间X (即当r<n时有πr(X)=0)，πn(X) 同构于n维同调群Hn(X)，其同构对应由自然对应Φn：πn(X)→Hn(X) 确立，这就是著名的胡雷维奇定理。以此为发端，代数拓扑学进入了同伦论研究的发展阶段，研究空间之间的映射的同伦分类以及空间的伦型分类成了代数拓扑学在这一发展阶段的中心问题。
继胡雷维奇定理之后，人们自然的提出了 (n-1) 连通空间的 (n+1) 和 (n+2) 维同伦群如何用同调群来确定，以及相关的 (n+1)，(n+2) 维多面体到 (n-1) 连通空间的映射的同伦分类问题。随着20世纪40年代以来斯廷罗德上同调运算的建立，为上述问题的解决提供了可能，上述问题成为50年代同伦论研究的主流课题。
40年代末至50年代初，陈省身在当时的中央研究院主持出版了多册代数拓扑论文集，把国外同伦论研究的动态介绍到国内来。周学光主要依靠自学，深入掌握了国外同伦论研究的文献知识，并首先抓住了当时同伦论的主流课题开展研究工作。
1953年，J. P. 塞尔 (Serré) 将胡雷维奇定理推广到 (n-1)C-连通空间。所谓 (n-1)C-连通空间X，即当r<n时有πr(X)∈C，其中C是某一非空的Abel群的族。在这个条件下，塞尔得出，自然对应Φn： πn(X)→Hn(X) 是C-同构，即ker Φn和imΦn∈C，塞尔没有得出关于Φn+r： ∏n+r(X)→Hn+r(X) 当r≥1的结论。周学光在1956年 《同伦群的关系及其应用》 的论文中推广了塞尔的结果。设Q表示正系数集而CQ表示这样一些群的集合，它的元素的阶数r有限且r的素因子都属于Q。对整数k，S(k) 表示所有满足2p-3≤k的素数p的集合。周学光在该论文中得出，对 (n-1)，CQ-连通空间X，Φm：πm(X)→Hm(X) 当n≤m≤2n-2时是CQUS(m-n)单同态而当n≤m≤2n-1时是CQUS(m-n-l)-满同态。这个结果给出了 (n-1) 连通空间X的πn+r(X) 和Hn+r(X) 当1≤r≤2n-2时一目了然的关系。由此还可得出当n≤m≤2n-2时πm (X) 的秩就是X的m维贝蒂(Betti) 数。周学光在1958年《同伦群和上同调群的上乘积》 的论文中又得出，对 (n-1) 连通空间X，πm(X) 的秩当 (2n-1)≤m≤3n-2时可以用X的贝蒂数和X的上同调群的上积结构不变量的适当关系式表示出来。这些结果引起国际同行专家的重视。
周学光的以上结果，得到了 (n-1) 连通空间X的πn+r(X)的丰富信息，但是，要完全确定πn+r(X) 以及 (n+r) 维多面体到 (n-1) 连通空间的映射的同伦分类问题，随着维数r的增加，则是更困难的问题。50年代初，张素诚先生，希尔顿(Hilton) 和庞特里亚金 (Pontrjagin) 各自独立的确定了πn+1(X)。1953年，S.艾伦伯格 (Eilenberg) 在国际拓扑学会议上提出了一些需解决的重要问题，其中有确定 (n-1) 连通空间X的πn+2(X) 的问题和 (n+2) 维多面体到 (n-1) 连通空间的映射的同伦分类问题。周学光在1959年《斯廷罗德运算和同伦群 (Ⅱ)》 的论文中完全确定了 (n-1) 连通空间X的πn+2(X)。根据周学光的前述结果，πn+2(X) 的秩数等于X的 (n+2) 维贝蒂数，πn+2 (X) 的p分量群当p为奇素数时同构于Hn+2(X) 的p分量群。因此问题只剩下确定πn+2(X) 的2分量群C(πn+2(X)，2)。周学光在该论文中得出C(πn+2(X)，2) 是群C(πn+2(X)，2)∩Φn+2-1 (0) 被群C(Hn+2(X)，2)∩ Sp2-1(0)的扩充，其中Sp2： Hn+2(X，Z2)→Hn(X，Z2) 为斯廷罗德同调运算。 论文还进一步用同调运算i指出了这个扩充的构造，从而完全确定了C(πn+2(X)，2)。值得指出的是，这里的同调运算i是周学光建立的新的第二类上同调运算i的对偶。
周学光在1959年 《同调群和连续映射 (Ⅰ)，(Ⅱ)》论文中解决了 (n+2) 维多面体Y到 (n-1) 连通空间X的映射的同伦类集合π(Y，X) 结构的确定问题。周学光在该论文中得出自然对应φ： π(Y，X)→A(Y，X，△，μ，Sq2) 是满同态，这里代数系统A(Y，X，△，μ，Sq2) 表示由Hn(Y) 到Hn(X) 的一族同态，它们与博克斯坦 (Bockstein) 运算△，怀特黑德同态μ和斯廷罗德运算Sq2可交换。论文还确定了核φ-1(0) 的构造，从而完全解决了这个分类问题。周学光完全解决了1953年国际拓扑学会议上提出的上述两个重要问题，获国内外同行专家的重视和高度评价。
纠正Shiraiwa定理的错误
在50年代，除了上述两个重要问题之外，还有一个确定Anr多面体伦型问题，也是当时同伦论的主流课题。所谓Anr多面体是指 (n-1) 连通的n+r维多面体，如何用它的上同调不变量确定它的伦型，是当时主流课题之一。
1948年，怀特黑德证明了An2多面体的伦型当n≥3时完全可由它的上同调系统确定。1954年，日本拓扑学家K. Shiraiwa在 “美国数学杂志” (American J. of Math.) 发表论文得出，An3多面体当n≥3时的伦型与上同调系统一一对应关系，而这个上同调系统中的一族同态只要求与斯廷罗德平方运算和阿德姆(Adem) 运算Ф1，Ф2可交换。这是当时著名的Shiraiwa定理。
周学光在1958年《Steenrod运算和同伦群 (Ⅱ)》 (科学纪录1958年11期) 的论文中举出反例说明了Shiraiwa定理不能成立，并指出只用到斯廷罗德运算和阿德姆运算Ф1，Ф2不足以确定An3多面体的伦型，还需要用到更多的第二类上同调运算。周学光在1959年 《斯廷罗德运算和同伦群 (Ⅱ)》 (数学学报1959年第3期) 的论文中建立了新的第二类上同调运算i， 并且在1960年 《同调群和连续映射 (Ⅰ) (Ⅱ)》 的论文中提出了Shiraiwa定理的正确表述并予以证明。在定理的正确叙述中，An3多面体的上同调系统的一族同态还应与周学光建立的第二上同调运算i可交换。
周学光关于纠正Shiraiwa定理的一系列论文的发表，在国际拓扑界引起广泛而强烈的反响。著名代数拓扑学家J. F. 亚当斯 (Adams) 在美国 《数学评论》 中用大量篇幅介绍周学光的工作。亚当斯在评论中认为所举的反例是正确的，但是对于第二类上同调运算i在A3n多面体伦型问题中的作用尚存疑问， 表示有待于看到更详细的证明之后才能予以肯定。周学光随后发表了?关于 “斯廷罗德运算和同伦群” 一文的声明》，对亚当斯提出的疑问予以详细说明。亚当斯在后来撰写的评论中表示认同。由此，周学光在国际代数拓扑界享有很高声望。H.J. 鲍斯(Baues) 在 《Algebraic Homotopy》 的专著中和在 《Topology》杂志发表的论文中引用了周学光的有关论文。日本拓扑学家Shimada在介绍上同调运算的一篇论文中称第二类上同调运算i为周的运算。
周学光在50年代的上述工作，系统而又创造性的解决了当时同伦论研究的一系列主流课题。著名前苏联拓扑学家波斯尼科夫在60年代所著《同伦论进展》一文中以大量篇幅介绍了周学光的系列工作。
建立特征上同调运算和上同调运算的基底
在60年代初，周学光对50年代的系统工作进行了概括并上升到更高的理论，建立了特征上同调运算理论。在1964年 《上同调运算和伦型 (Ⅰ)》 中，周学光对任意空间Y，X和正整数n≥2建立了特征上同调运算Tn。这是多值的上同调运算，它的定义域为Y-系列上同调群的直和
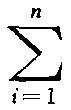Hi(Y，Hi(X))， 而取值域为Y的上同调群Hn+1(Y，Hn+1 (Xn))，其中Xn为X的高度为n的同调分解。周学光在该论文中利用特征上同调运算得出了具有更高概括性的定理。定理指出，当X维数≤n+1或Y维数≤n+1且X单连通，则由X到Y的上同调系统中的一族同态λ有几何实现当且仅当这一族λ与博克斯坦运算△，怀特黑德同态μ和特征上同调运算Tn都可交换 (简称为λ是△-μ-Tn-同态)。另外一个定理又指出，当X，Y都是单连通的而且X，Y维数都≤n+1，则X，Y有相同伦型当且仅当X，Y的上同调系统中的一族同态λ是△-μ-Tn-同构。这一结果统一了波斯尼科夫和?特黑德关于Anr多面体伦型问题的两种不同的理论。周学光在?上同调运算和伦型 (Ⅱ)》 中利用斯廷罗德和庞特里亚金运算，上乘积和阿德姆运算计算了 (n-1) 连统且高度为n+1和n+2的空间的特征上同调运算，得出了关于An2多面体伦型的怀特海定理和关于An3多面体伦型的Shiraiwa定理 (以正确的形式) 的很简单的证明。这就完全实现了关于Anr多面体伦型问题的两种不同理论的统一，引起国际代数拓扑界的重视。在60年代，周学光还有两项重要结果。在 《关于上同调运算的基底》 中，在无限多种上同调运算的集合中建立了一组基底，使任一上周调运算都可以用这一组基底上同调运算唯一的表示出来，大大简化了无限多种上同调运算之间的关系。在《Pontrjagin Thomas幂运算和对称群的同调》 (中国科学 (通讯) 16卷第2期) 中完全确定了对称群S(m) 的同调群Hx(S(m))，它的p分量群同构于一种可计算的链复形的同调群。作为这个结果的应用，周学光还得出了球面的对称乘积的同调群的明显表达式。
向球面同伦群的研究迈进
进入80年代以来，周学光加强了同国外同行专家的交流。1987年赴美国参加Arcate国际代数拓扑会议，1989年再次赴美国伯克利 (Berkeley) 数学研究所参加代数拓扑学术年活动。在80年代初，周学光在广义上周调群的计算以及广义同调群及其系数群的关系等方面取得一系列有益的结果。在1981年 《差不多闭流形的嵌入定理》 的论文中，周学光证明了一个重要定理。定理指出，如果W是n维k连通的差不多闭的流形，1≤k<n/2，h为正整数使k≤2k，2n-k>5而且存在W上一个 (n-h-1)维向量丛v使它s等价于W在 (2n+1) 维欧氏空间微分嵌入的法向量丛，则W可整齐的嵌入到2n-h维圆盘D2n-h。这个定理的条件具有一般性，而所嵌入到的D2n-h的维数2n-h尽可能的低，统一了前人关于嵌入问题的认识。周学光在该论文中将这个结果应用到 (m-1)2m，2m+1，2m+2维差不多闭流形的嵌入问题中，具体确定了嵌入到的圆盘D2m+r的维数2m+r(某个与m有关的正整数r)，是各种文献得到结果中最低的。
在80年代后期，周学光开始从事球面同伦群的研究，这个课题是同伦论的中心问题之一，也是几十年来众多拓扑学家为之奋斗的世界公认的经典难题。在1988年 《发觉同伦类的高阶上同调运算》 的论文中，周学光在斯廷罗德代数A的上同调ExtA的计算方面建立了一种有序链复形的方法，使庞杂的计算变得有规律可循且予以简化。塞利克 (Selick) 在美国 《数学评论》 的评论认为此方法为首创。斯廷罗德代数的上同调ExtA的计算??般是通过共棒复形B(A) 的同调群来计算，而B(A) 生成元的构成很复杂，一般是一种单项式的和，而每个单项式又是由Ax(A的对偶) 的多个生成元的幂的张量积组成，非常庞杂，令人望而生畏。通过这种有序链复形方法，可对B(A) 作出商链复形C(A)，使C(A) 的同调群和B(A) 的同调群一致，而C(A)的生成元是B(A) 生成元中诸多单项式的首项，使计算得以化简。利用这个方法，周学光在该论文中计算出ExtA中β1，β2和h0hn(或h0bn) 之间的乘积或者梅西 (Massey) 乘积是非零的。再利用亚当斯谱序列的有关结果，论文又得出球面稳定同伦群中的β1，β2和由h0hn表示的科恩-格尔斯元素ηn (或由h0bn表示的科恩元素ζn) 之间的乘积或者户田乘积是非平凡的，得出了无穷多族球面稳定同伦群中的新元素，大大丰富了对球面同伦群的认识。周学光关于差不多闭流形的嵌入定理等成果获1985年国家教委优秀成果奖，《发觉同伦类的高阶上同调运算》 等论文成果于1991年获国家教委科技进步奖。
周学光培养了硕士和博士研究生20余名，为我国同伦论及其应用的研究培养了一批骨干。周学光对每一位学生，在生活上给予热情关怀，在学习和完成论文的过程中不遗余力地热情指导并予以严格要求。周学光以严谨的治学作风言传身带，使每一位学生深受感染。周学光具有渊博的知识和敏锐的思想，使每一位学生深感敬佩并因此而得益匪浅。目前，在他的带领下，在南??大学数学系形成了一个研究集体，在同伦论及其应用的许多领域开展研究工作，近10多年来已发表数十篇高水平的论文。
简 历
1927年6月5日 出生于四川省资中县。
1948年6月 毕业于成都市四川大学数学系并留校任教。
1950年 在南开大学数学系任教。
1952年起 在南开大学数学系历任讲师 (1952); 副教授 (1978)，教授
(1979)。经国务院学位委员会评定为我国第一批博士研究生导师 (1981年)。
1981—1983年 任南开大学数学系副系主任。
1984—1987年 任南开大学数学系系主任。
1987—1996年 任中国数学会天津分会副理事长、理事长。
1954年加入中国民主促进会。
1992年任国家自然科学基金委员会数理学部专家评议组成员。
1990—1995年 国家教委高等学校教学指导委员会基础数学指导组成员。
主要论著
1 周学光. 关于Borsuk的绝对同伦扩张性质的讨论. 数学学报，1956，6(2)： 233—241
2 周学光. 同伦群和同调群的关系及其应用. 数学学报，1958，7 (2)：346—370
3 周学光. 同伦群和同调群的上乘积. 数学学报，1958，8 (2)：200—209
4 周学光. Steenrod运算和同伦群 (Ⅱ). 科学纪录，1958，新2 (11)：419—423
5 周学光. Steenrod运算和同伦群 (Ⅰ). 数学学报，1959，9 (3)：227—242
6 周学光. Steenrod运算和同伦群 (Ⅱ). 数学学报，1959，9 (3)：242—266
7 周学光. 同调群和连续映射Ⅰ. 广义同伦群和Shiraiwa定理. 科学纪录，1960，新4 (3)： 139—144
8 周学光. 同调群和连续映射Ⅱ. (n+2) 维多面体到 (n-1) 连通空间的同伦分类. 科学纪录，1960，新4 (3)： 145—152
9 周学光. 关于 “Steenrod运算和同伦群 (Ⅱ)” 一文的一点声明. 数学学报，1963，13 (4)： 544—547
10 周学光. 上同调运算和同伦群. 数学学报，1964，14 (6)： 849—860
11 周学光. 上同调运算和伦型 (Ⅰ); (Ⅱ) (英文稿). 中国科学，1964，12 (7)： 1019—1031; 1032—1043
12 周学光. 关于上同调运算的基底 (英文稿). 中国科学，1965，13 (7)
13 周学光. Pontrjagin-Thomas幂和对称群的同调群. 中国科学 (通讯).1966，14 (2) 297—299
14 周学光. 差不多闭流形的嵌入定理. 数学学报，1981，24 (8)：920—928
15 周学光. 广义同调群及其系数群的关系 (英文稠). 中国科学 (A辑)，1983，24 (9)： 909—918
16 周学光. 广义上同调群和Postnikov不变量. 数学学报，1984，27(5)： 684—693
17 周学光. 纤维空间和纤维丛. 科学通报，1984，24 (6)： 95—96
18 周学光. 发觉同伦类的高阶上同调运算 (英文稿). Lect. Notes in Math.，1988，1370： 416—436
相关参考
周学熙（汉语拼音：ZhouXuexi，1866～1947），中国实业家。字缉之，别号止庵。安徽东至人。1947年9月26日卒于北平（今北京）。其父周馥曾任山东巡抚、两江总督、两广总督等职。周学熙1
开办直隶工艺总局，是袁世凯推行“新政”的重要内容。光绪二十九年(1903)3月，袁世凯派周学熙到日本考察工商业。回国后，周学熙根据自己所见、所闻、所感、所思，写成《东游日记》，讲了日本的富强，是由于搞
周学霆拗不过他，就推托说没有开方的纸笔，在路边捡了一个红色的小石子，在一块大石头上写了几行字，要他背着这块大石头到山下去找药店配药，中途不可停歇，越快越好。>清嘉庆、道光年间，湖南邵阳出了个神医周学霆
王珞丹(1984年1月30日-)，内地女演员，毕业于北京电影学院表演系本科。2007年，王珞丹因在赵宝刚导演的青春励志剧《奋斗》中出演“米莱”而走红。2008年，再次在赵宝刚的电视剧《
王琼是明朝的军事人物，他经历了成化、弘治、正德和嘉靖四个皇帝，从六品官做到了户部、兵部和吏部尚书一品大员，王琼生平有三大功绩为人所称赞，一是治理漕河;二是，平定宸濠叛乱;三是，总制西北边防。人物简介>
葛洪，晋朝时代的医学家、博物学家和制药化学家，炼丹术家，著名的道教人士，人称葛仙翁，他在中国哲学史、医药学史以及科学史上都有很高的地位。人物简介>葛洪是中国东晋时期有名的医生，字稚川，自号抱朴子，丹阳
葛洪，晋朝时代的医学家、博物学家和制药化学家，炼丹术家，著名的道教人士，人称葛仙翁，他在中国哲学史、医药学史以及科学史上都有很高的地位。人物简介>葛洪是中国东晋时期有名的医生，字稚川，自号抱朴子，丹阳
历史人物 王珞丹个人资料_王珞丹人物简介,王珞丹个人资料_王珞丹人物简介
王珞丹个人资料_王珞丹人物简介 中文名：王珞丹 英文名：May 国家或地区：中国内地 生日：1984-01-30 出生地：内蒙古自治区赤峰市 职业：演员 星座：水瓶座
历史人物 王珞丹个人资料_王珞丹人物简介,王珞丹个人资料_王珞丹人物简介
王珞丹个人资料_王珞丹人物简介 中文名：王珞丹 英文名：May 国家或地区：中国内地 生日：1984-01-30 出生地：内蒙古自治区赤峰市 职业：演员 星座：水瓶座
·姚錱个人人物简介姚錱，实验形态学家，细胞生物学家，实验肿瘤学家。毕生围绕着细胞的生长和分化及其调节控制这一重大的生物学问题，或从正常的发育，或从肿瘤细胞异常的分化深入探索，在基础研究和应用研究两方面