知名人物 李国平人物简介
Posted 函数
篇首语:花门楼前见秋草,岂能贫贱相看老。本文由小常识网(cha138.com)小编为大家整理,主要介绍了知名人物 李国平人物简介相关的知识,希望对你有一定的参考价值。
知名人物 李国平人物简介
·李国平

李国平,数学家。长期从事函数论研究,在整函数与半纯函数理论,解析函数逼近论,准解析函数理论等领域获众多成果。他积极倡导数学物理研究,并创办了专门杂志。
李国平,幼名海清,字慕陶。1910年11月15日生于广东省丰顺县沙田黄花村。其父善长裁缝手艺,前妻不幸早故; 继室郑若川女士,生有五子二女。
李国平少时家贫,10岁前读私塾,启蒙老师为丰顺著名学者李福田先生。11岁时由伯父李介承带往广州,进当时的南海第一高小学习,后又考入中山大学附中的前身广东省高等师范附中。入学时成绩优异,唯数学仅15分而甚苦。初中二年级开始,得刘君罴先生授以自学之法,并赠《温德华氏小代数》书,勉其自励,精心指点,有所领悟,自此酷爱数学,逐步奠定了他毕生学业的基础。从17岁进高一到大学毕业的7年时间,他又为生计所迫,半工半读。
李国平1933年毕业于中山大学数学天文系。大学期间受到赵进义、刘俊贤两位著名教授的栽培。毕业后即受聘于广西大学数学系任讲师。1934年至1936年东渡日本,在东京帝国大学读研究生,得到系主任竹内端三及辻正次教授的指导。在此期间,因文会友而与我国数学界的前辈熊庆来结为忘年交。1937年经熊庆来提名推荐任中华教育文化基金会研究员,派赴法国巴黎大学庞加莱(Poincaré)研究所工作。1939年抗日战争初期,国家民族处于危难之际,他毅然回国。其后他历任四川大学数学系教授,武汉大学数学系教授、系主任、副校长、校务委员会副主任、数学研究所所长,中国科学院数学计算技术研究所所长,中国科学院武汉数学物理研究所所长,国家科学技术委员会武汉计算机培训中心主任,湖北省科学技术协会副主席、顾问,国家科学技术委员会数学学科组成员,中国数学会理事,中国系统工程学会副理事长兼学术委员会主任,中国数学会名誉理事,湖北省暨武汉市数学会名誉理事长,中国科学院武汉数学物理研究所名誉所长,《数学物理学报》 主编,《数学年刊》副主编,《数学杂志》及《系统工程与决策》名誉主编。1955年当选为中国科学院学部委员。1956年加入中国共产党。曾被选为全国先进工作者,是第四、第五、第六届全国人民代表大会代表。
李国平早在青年时期,就以函数论为其研究方向,自1935年起陆续发表了一批关于半 (亚) 纯函数方面的研究成果,受到著名函数论专家G.瓦利隆(Valiron)的注意,并逐篇加以评介,发表在德国 《数学及其边缘学科文摘》上,前后有6篇之多。在整函数与半纯函数理论中,除R. H. 奈望林纳(Nevanlinna)的示性函数外,级与型是关键性的概念。1936年,他剖析了L. O. 布卢门塔尔(Blumenthal)关于函数型的理论,在奈望林纳、瓦利隆、H. 米洛 (Milloux)、劳赫 (Rauch) 等人工作的基础上,提出了半纯函数(有限级与无限级)的波莱尔 (Borel)方向与填充圆的统一理论,其中特别包括了他在1935年与熊庆来用不同方法同时建立的无限级半纯函数理论。熊庆来在 《亚纯函数的几个方面的近代研究》一文中就曾经指出:“关于奈氏的学理……在我国方面亦先后有我自己及李国平、庄圻泰等的一些工作,其中关于无穷级的函数者尤较具体而显著。”瓦利隆在其《半纯函数的波莱尔方向》一书中也肯定了这一点。熊庆来在上文中还对李国平关于半纯函数理论研究中的另一贡献——辐角分布理论作了充分肯定。这一工作已收入李国平的专著中。他关于奈望林纳第二基本不等式中的重级指量N1 (r)的进一步探讨也是重要的。熊庆来在《十年来的中国科学(数学部分),1949—1959》的《亚纯函数论与解析函数正规族论》一文中就指出,李国平凭借他对上述奈望林纳基本不等式的强化,就填充圆与波莱尔方向,得出了较瓦利隆与米洛的定理更为精密的结果。在这篇关于中国数学发展历史的文献中,对李国平在唯一性问题、有理函数表示问题、整函数论在函数序列的封闭性问题上的应用、伴随外尔斯特拉斯 (Weier-strass) 函数及强伴随外尔斯特拉斯函数等方面的研究作了评述。
李国平还研究了解析函数逼近等问题。例如他利用布特鲁-嘉当 (Boutroux-Cartan)定理获得了整函数的拉格朗日 (La-grange)插值收敛性的一些结果、关于解析函数用费伯(Faber)多项式逼近的一些结果等。这些工作在《十年来的中国科学 (数学部分),1949—1959》一书中均有介绍。
在准解析函数类的研究方面,他在40年前即有两篇与此有紧密联系的论文由P.蒙泰尔(Montel)推荐发表在巴黎科学院院报上。由于战争环境的影响,这方面的研究工作被迫中断; 直至抗日战争胜利后,他才得以回到这一领域继续其研究工作,并在武汉大学理科季刊上发表了一批关于概周期函数的准解析性的判定准则,其中典型的结果在美国《数学评论》(1959年第10期,701页) 上有所介绍。
由于他早期专攻复变函数论并希望探索一条数学理论联系实际的道路,因此,他一直关心微分方程的解析理论以及这门学科的广泛应用背景。在这方面,他从40年代起即影响了一些学生,让他们注意这一领域的研究及进展。中华人民共和国成立后,李国平着意建立一支微分方程的研究队伍。为此,1954年他受教育部委托,与申又枨、吴新谋等合作,在北京举办了微分方程讨论班。他与申又枨主讲常微分方程的理论部分,为在我国建立微分方程的研究队伍做出了贡献。这一时期,他研究了与此有联系的自守函数、闵可夫斯基-当儒瓦(Minkowski-Denjoy)函数的问题,着重研究了复变量的闵可夫斯基-当儒瓦函数问题,所得结果已收集在专著中。
此外,他将自己关于半纯函数、整函数与准解析函数的研究成果应用于常微分方程和差分方程的研究中,并研究了将函数构造理论的结果应用到微分方程理论中的问题。他还在国内外一些刊物上发表了一系列函数论方面的其他论文,包括函数构造理论的转化原则(间接方法与直接方法)、等角写像边界性质、全纯函数的边界性质、柯西 (Cauchy)型积分与奇异积分方程方面的普里瓦洛夫 (Привалов)定理 (或其推广)及其对弹性理论的应用,以及准解析函数与半纯函数理论对某些差分方程组的应用、拓扑群上的函数理论、普遍二重级数、半纯函数的反函数等新的研究成果。特别是最近几年,他完成了 《准解析函数论》、《推广的黎曼几何在偏微分方程中的应用》、《算子函数论》、《亚培尔函数论》等多种专著。这些都是他本人30年代工作的继续,对前人相应的工作都有所推进。
1956年,李国平出席了全国12年科学远景规划会议,是数学组、计算技术组、半导体组和自动化组的成员,还是函数论规划的起草人。自此,他对祖国的未来更加充满信心,对各学科之间相互联系,相互渗透的科学技术发展趋势有了进一步的深刻认识。60年代后,他毅然把注意力转向数学对国民经济与国防建设的实际应用,积极倡导数学同其他科学技术的边缘研究,大胆地提出了一种现在常被形象地称为“一个主体、两个翅膀”的科研设想。主体是数学、计算机科学与系统科学的三结合,发展数学、应用数学与计算数学,并开发系统科学的基础理论; 一支翅膀是数学与物理科学相结合(包括天文、地学、化学以至工程技术),研究宇观、宏观与微观物理现象的数学规律性,为物理科学乃至工程技术服务; 另一支翅膀是数学与生物科学相结合,研究运动形式的发展,特别是生物运动与生命运动的数学规律性,为生物科学乃至系统科学服务。他希望以此为线索探求数学应用的具体途径,并为纯数学提供新的内容、概念与方法,发展数学本身。
为了实现这一宿愿,他毅然部分地中断了他所熟悉的函数论方面的研究,30年如一日,含辛茹苦地勤奋工作,在数学物理与系统科学两个领域为应用数学与数学的应用开辟新路,取得了一些重要成就。1961年开始,他在电磁流体力学中从小扰动电磁流体力学波方程与传输线方程的相似性出发,提出了电磁流体力学波的特性阻抗概念,认为可以类似于电磁波中特性阻抗的作用,建立关于电磁流体力学波的工程理论。1976年,他在研究地震的弹性波方程时使用同样的观点导出了地震弹性波的特性阻抗,探索了地震弹性波传播的工程理论。这在 《数理地震学》 的第一章中有详尽的论述。从此,他所提出的英文名词“mathemtical seismo-logy”成为数理地震学公认的正式名称。
1965年间,他将纤维丛理论应用于基本粒子理论的研究,提出了纤维丛的微积分概念以探讨基本粒子的内外运动,所得结果被发表在《一般相对论量子场论》 中。这工作的思想要点是: 分别以狭义相对论与广义相对论描述基本粒子的内运动与外运动,前者的方程在经纤维丛积分后即可转化为后者的方程。由于狭义相对论的麦克斯韦(Maxwell)方程可以有两种方式被推广为广义相对论的麦克斯韦方程,这种转化当然也是一变为二的。可以认为,这种一变为二是由外运动而引起的。据此,他大胆地提出了一个猜想: 光子的反光子并不是它自身; 由外运动引出的两种方程是分别描述正反两种光子的。目前所观察到的两者的同一性,很可能是我们尚未获得观察广义相对论性效应的客观条件的结果。这是与其他广义相对论性理论实验证明的预言相一致的,但有待于星光近日是否弯曲并获得两种数据的观测结果以证明它的最后真实性。
李国平在1964年带领学生参加葛洲坝工程建设之后,针对岩土力学的研究引进了地质点的概念,提出了岩石统计力学的理论框架。1972年为了解决一位物理界的朋友提出的半导体各向异性能带问题,他以外微分形式为工具,系统地论述了现代数学物理中的8个分章内容,通过带关键性的半导体中导带电子有效质量张量
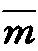
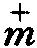
正是通过这漫长而艰苦的奋斗过程,他不仅自身孜孜不倦忘我劳动,写了近80篇学术论文,在已出版的《函数论》、《数学物理》与 《系统科学》三套丛书中,他撰有《半纯函数的聚值线理论》、《自守函数与闵可夫斯基函数》、《电磁风暴说》、《数理地震学》、《导体与半导体》、《一般相对论性量子场论》(Ⅰ与Ⅱ)、《推广的黎曼几何方法及其在偏微分方程中的应用》、《亚培尔函数论》、《算子函数论》以及《数学模型与工业自动控制》(1—3卷)等共18部专著。李国平先后参与创建了中国科学院武汉数学物理研究所、数学计算技术研究所、国家科委计算机培训中心等科研机构,创建或恢复了 《数学物理学报》、《数学杂志》、《数学年刊》、《数学通讯》等学术刊物以及中国系统工程学会、湖北省系统工程学会、湖北省暨武汉市数学会等学术组织;1979年与1982年他亲自组织主持召开了全国第一、二次 “数学物理学术讨论会”,为形成上述研究领域蓬勃兴起的大好形势作出了积极贡献。
李国平为我国的科学事业执著追求,奋斗不息,同时为发展我国的教育事业亦怀着 “登高人向东风立,捧土培根情更急”的圣洁之情,为我国培养和造就了一批优秀专家学者,近百名教授是他的高足,更多的中青年在他的指导下迅速成长。
李国平毕生成就的另一方面是他数十年间撰写数百首诗词。早在中山大学攻读数学天文时,即兼修了中文系的古代文学等课程,对古典诗词产生了浓厚兴趣,含英咀华,打下了深厚基础。他的诗词之作题材丰富,笔力雄健,意境清新高远,语言朴实生动,铿然有金石声,如骊龙之珠抱而不脱,耐人寻味之作比比皆是。整个诗词确是他胸怀、心灵的写照,是作为科学家的良心与艺术家心灵相结合的体现。
李国平教授于1996年2月8日在武汉病逝,享年86岁。
简 历
1910年11月15日 出生于广东省丰顺县。
1923—1926年 在中山大学附属中学学习并兼任南方中学数理化教师。
1927—1929年 在中山大学预科学习。
1929—1933年 在中山大学数学天文系学习。
1933—1934年 任广西大学数理系讲师。
1934—1936年 日本东京帝国大学理学部数学科研究生。
1937—1939年 任中华教育文化基金会研究员赴法国巴黎大学庞加莱研究所工作。
1939—1940年 任四川大学数学系教授。
1940—1996年 任武汉大学数学系教授。
1955年 被聘为中国科学院学部委员 (1994年改称为中国科学院院士)。
1956年 当选为全国先进工作者。任第四届至第六届全国人民代表大会代表。
1956—1968年 任中国科学院武汉数学研究室主任,中国科学院数学计算技术研究所所长。
1977—1984年 任武汉大学副校长、校务委员会副主任、数学系主任、数学研究所所长。
1979—1986年 任中国科学院武汉数学物理研究所所长,国家科委武汉计算机培训中心主任。
1979—1996年 任 《数学物理学报》主编。
1986—1996年 任中国科学院武汉数学物理研究所名誉所长。
1991—1996年 任中国科学院武汉物理研究所波谱与原子分子物理国家重点实验室研究员与顾问。
1996年2月8日 在武汉病逝。
主要论著
1 李国平. 半纯函数的聚值线理论. 北京: 科学出版社,1958.
2 李国平,郭友中,陈银通. 自守函数与闵可夫斯基函数. 北京:科学出版社,1979.
3 李国平,郭友中. 数理地震学. 北京: 地震出版社,1978.
4 李国平.一般相对性量子场论Ⅰ,Ⅱ.武汉:湖北人民出版社,1980;1981.
5 李国平. 数学模型与工业自动控制1—3卷. 武汉: 湖北人民出版社,1978; 1980; 待发表.
6 李国平. Bessel函数的性质. 中山大学自然科学季刊,1930.
7 Li Guoping.On meromorphic functions of infinite order.Jap.J.Math.,1935,12: 1—16.
8 Li Guoping. On the unified theory of meromorphic functions. J. Fac.Univ.Tokyo sect.,1937,13: 153—286.
9 Li Guoping.Sur les valeurs multiples et les directions de Borel des fonctions meromorphis. C. R. Acad. Sci.,Paris,1938,209:1548—1550.
10 Li Guoping. Sur un theoreme fondamental dams la theorie des fonctions quasi-analytiques. C. R. Acad. Sci.,Paris,1939,208:1625—1627.
11 Li Guoping. Sur des nouvelles classes quasi—analytiques des fonctions.Ibid,1939,208: 1783—1785.
12 李国平.关于具特征函数之非线性常微分方程的新理论.数学学报,1954(4): 467—478.
13 李国平. Привалов氏定理. 武汉大学自然科学学报,1956 (1): 5—10.
14 李国平.Riesz氏定理的转化形式. 数学学报,1957,7 (1): 128—131.
15 李国平. 整函数插补法中一个基本定理. 数学学报,1957,7 (2):268—270.
16 李国平. Cauchy氏不等式的转化形式. 数学学报,1957,7 (3): 340—345.
17 李国平.解析函数构造理论中两个基本原则及其推广.数学学报,1957,7 (3): 327—339.
18 李国平. 函数论中的若干问题. 中国科学院武汉分院建国三十周年论文集,1980.
19 李国平.Fourier变式、梅林变式及其应用.中国科学院计算技术研究所,1958.
20 李国平. 外微分形式在数学物理中的应用 (Ⅰ)—(Ⅲ). 全国数学物理座谈会报告,1977.
相关参考
20世纪上半叶的中国风云激荡,无数仁人志士为争取民族独立和人民解放抛头颅、洒热血,树立了一座座巍峨的英雄丰碑,袁国平就是其中一位杰出代表。从1925年10月考入黄埔军校第4期政治科,同年加入中国共产党
汉神爵元年(公元前61年)四月至十一月,汉后将军赵充国平定西羌的一次大规模进攻战。 神爵元年春,以先零羌为首的西羌各种反汉。四月,汉宣帝遣后将军赵充国率骑兵万余人前往镇压。赵充国兵抵金城(今甘肃
汉神爵元年(公元前61年)四月至十一月,汉后将军赵充国平定西羌的一次大规模进攻战。 神爵元年春,以先零羌为首的西羌各种反汉。四月,汉宣帝遣后将军赵充国率骑兵万余人前往镇压。赵充国兵抵金城(今甘肃
解忧公主是谁的女儿呢?刘解忧出身西汉皇族,祖父是楚王刘戊,也曾雄霸一方,但是历史上对于刘戊的子女并没有记载,所以刘解忧的父亲是谁也就不得而知了。但是后来刘戊参与了“七国之乱”,结局是兵败自杀,留下了一
解忧公主是谁的女儿呢?刘解忧出身西汉皇族,祖父是楚王刘戊,也曾雄霸一方,但是历史上对于刘戊的子女并没有记载,所以刘解忧的父亲是谁也就不得而知了。但是后来刘戊参与了“七国之乱”,结局是兵败自杀,留下了一
袁国平(1906年一1941年),湖南宝庆(今邵阳)人。原名袁幻成,又名袁裕,字醉涵,笔名最寒。袁国平同志是忠诚的共产主义战士,杰出的无产阶级革命家,中国工农红军和新四军的高级指挥员、卓越的政治工作领
读哲学,做一个有灵魂的人——周国平给中学生的阅读建议周国平,著名诗人、作家、哲学家。1945年生于上海。1962-1968年就学于北京大学哲学系,毕业后分配在广西深山老林中。1978年考入中国社会科学
在我军的历史上,皖南事变绝对是一次极其惨重的损失。>当时,新四军9000多人在国民党军80000人的围攻下,大部分壮烈牺牲,新四军的最高领导层:军长叶挺被俘,政委项英、参谋长周子昆、政治部主任袁国平全
在我军的历史上,皖南事变绝对是一次极其惨重的损失。>当时,新四军9000多人在国民党军80000人的围攻下,大部分壮烈牺牲,新四军的最高领导层:军长叶挺被俘,政委项英、参谋长周子昆、政治部主任袁国平全
邹忌从与城北徐公比美这件事总结出的经验教训,认为对帝王治国平天下也有促进作用,邹忌在向齐王进谏的时候,也没有单刀直入,而是巧妙的借用自己的亲身体会,通过类比的方式。从小家到大家,管理国家与管理家庭有异