知名人物陈希孺人物简介

Posted 2022-04-04 线性

篇首语：重要的不是发生了什么事情，而是要做哪些事来改善它。本文由小常识网(cha138.com)小编为大家整理，主要介绍了知名人物陈希孺人物简介相关的知识，希望对你有一定的参考价值。

知名人物陈希孺人物简介

·陈希孺

陈希孺，数学家。主要从事数理统计的研究。他在统计工作中深入应用分析数学工具，一些估计达到较高精密程度。他在线性回归大样本理论，非参数理论等方面都有贡献。他长时间在中国科学技术大学工作，培养与影响了不少数理统计学家。

陈希孺1934年2月11日出生，湖南望城县人。1956年9月毕业于武汉大学数学系。1980年在中国科学技术大学晋升为数学系教授，1981年被批准为首批博士生导师。曾任中国数学会理事，中国概率统计学会理事长，现为中国科技大学研究生院(北京) 教授，中国现场统计研究会理事长。他曾多次应邀赴美、加、日、港、台访问或参加国际会议。1986年，因其突出贡献被遴选为国际统计学会 (International Staistical Institute) 的成员 (Member)。1991年5月当选为中国科学技术协会第四届全国委员会委员。曾任《应用概率统计》杂志主编，现为《中国科学》、《数学年刊》、《系统科学与数学》及国际性统计刊物 “Statistica Sinica” 的编委。

陈希孺的老家在长沙市北20千米处一个名叫陈家塅的地方，祖父务农，父亲上过新学校。陈家塅滨临湘江，山环水抱，一派田园风光，离开长沙虽不算远，但当时仍很闭塞。上小学时他体弱不好动，当同龄的孩子们热心于爬树、游水、捉鱼、采野果之时，他常在家中埋头看书，并从中得到了乐趣。1946年秋考入长沙市长郡中学。长沙的中学质量，在国内应属上乘，他的数学老师如喻斗琪先生、杨少岩先生等，在省城甚有名气，都是一时之选。在他们的指点和影响之下，他对数学的兴趣与日俱增，萌生了选择数学作为终生专业的想法。

在报考大学之前，他的父亲和姐姐相继病故，因家计窘迫，他曾打算中学毕业后去小学任教，幸而当年政府宣布了大学生吃饭不收费，才得以勉力进入大学之门。1952年秋他顺从母意就近考入湖南大学数学系，一年后因院系调整转到武汉大学数学系，1956年毕业，分配到中国科学院数学研究所工作。当时因12年科学规划的考虑，概率统计组大扩张，当年分配到所的毕业生，绝大多数进入该组，他也在其列。他在大学时未修过这方面的课程，不能不 “从零开始”，一方面去北大听王寿仁先生和张里千先生讲授的基础课程，一方面自学几本著作，夜以继日，紧张学习了一段时间，打下了初步基础。可惜的是，接着一连串的事件打乱了这一进程。先是1957年秋他被选派去波兰留学，原定3年，后因反右运动中的牵连，在1958年10月提前调回国内，又于1959年下放陕西洛川劳动1年。直到1961年春调至新成立不久的中国科技大学任教，才有了一个较为安定的环境。

中国科技大学建立于1958年，在 “全院办校，所系结合”的口号下，中国科学院内一大批学术造诣深的专家来校兼课，阵容很强。相对而言，概率统计专门化就显得较为薄弱。“文化大革命”前，在59，61和63级开设过这一专门化。任课教师中，除王寿仁、张里千等资深专家外，大多数是像陈希孺这种经历，边教边学。他讲授过从基础到专业的大量课程。当时的努力现已得到了回报，如今科学院 (包括中国科技大学在内) 概率统计方面的学术带头人和骨干力量，不少是这几个年级的毕业生，其中一些人取得了具有国际影响的成果。当时教材缺乏，多数课程得自编讲义，任务繁重，因此1961年至1962年，他的主要精力都放在教学上。到1962年下半年，他才开始有余力顾及科研工作。首先是补基础，他选择了三四本名著仔细阅读，并把功夫主要下在大量地、系统地做习题上，包括其中一些很难的习题，全都逐一做了写在本子上。他常说，为了做这些习题，1963年，1964年两年的春节他没有下过楼。他认为多作习题，尤其是多作难题，对掌握和熟练本学科基本的论证方法和技巧，有着不可替代的重要性; 这方面修养的深浅，直接关系到攻克难点时能否产生别出心裁的想法，关系到日后科研工作的深入与否。他在编写的许多著作的序言中都强调了这一思想，书中所附习题很多出于自编，其中精彩的不在少数。另一方面，他自1962年秋参加了成平先生在数学所主持的一个参数估计的讨论班。参数估计是数理统计学的一个最重要的基础分支，二战前已有了初步的发展，到20世纪50年代，其热门是基于A. 瓦尔德 (Wald) 的统计决策理论而引进的一些新概念和新问题。凸损失的引进打破了平方损失的局限，minimax估计、同变估计和容许性等新概念拓展了估计优良性的研究范围和深度。当时成平是国内这个领域的学术带头人，他在minimax估计和容许估计方面，作出了具有国际先进水平的重要成果。陈希孺在这方面也取得了一些有重要意义的成果，突出的有：他解决了一般同变损失下位置-刻度参数的序贯(及蜕化为固定样本情形) minimax同变估计的存在和形式问题，此问题以往只在平方损失这个特例下解决过。他解决了在种种抽样机制之下，一般参数存在精确区间估计的条件，还否定了国外学者关于这个问题的一个猜测。应当说，成平和他在这个领域的成就代表了当时我国的水平，在国际上有一定的影响。他后来常常回忆起这段经历，感谢成平先生把他引进这个班，认为这是他学会独立进行统计研究工作的起点。到1966年，他已顺利地在几个领域开展了研究，发表了论文10余篇，在统计界初露头角。

在十年 “文化大革命” 中，除了一般大环境的影响之外，他还受到了比许多人更大的冲击。其实当时他是个 “四不” 人物：不参加组织，不参加串联，不写大字报，不参加集会。但他好发议论，问题就出在这里。他成了揭发和批斗的对象。所幸的是，他生性豁达，在逆境中能泰然处之，下午开他的批斗会，晚上有电影照样看，夜里也睡得很香。“文化大革命” 虽则中断了他的研究工作，但到未影响他的健康，反倒治好了以前因工作过度引发的神经衰弱。

“文化大革命” 结束后，他感到形势逼人，10年的中断使他原来掌握的学科基础落伍了。例如为掌握大样本统计的工具，“文化大革命” 前只要有洛易甫的《概率论》一书就基本够了，现在则有许多新发展，新工具，需要去补学。在研究课题方面，“文化大革命”前他熟悉的那些方向有的已归沉寂，有的已大大向前推进了，不易跟上。为了重新开始工作，从1978年开始的四五年内，他平均每天工作14小时以上。例如他了解到比灵斯利的《概率测度的收敛》很重要，国内当时仅北京图书馆有一孤本，且限借1个月，他用不到1个月的时间读完了该书并全文译出。读弗里德曼 (Freedman) 的《布朗运动与扩散过程》等书的情形也大致如此。他这些译稿都曾印出并在一定范围内流传。他汲取知识的那种迫切性，用 “如饥似渴” 来形容一点也不过分。通过努力，他更新了必备的基础，为新一轮研究做了准备。如何选择研究课题，当时对他来说是一件大事。他的成功之处在于能扬长避短。他先后开展过数理统计学中四五个领域的研究工作，以线性回归大样本理论和非参数统计中的若干方面为主，这些研究主要使用分析方法与概率极限理论，这是他比较擅长的方面。这些分支的研究开始于六七十年代，历史不算长，较易迎头赶上，有意义的问题也比较多。

通过多年的辛勤耕耘，陈希孺不仅在科学研究上取得了令人瞩目的成就，而且带领培养和联系了一批人投入研究工作，推动了我国数理统计学科的发展。到目前为止，他已在国内外学术刊物发表论文100多篇，出版专著和教科书11本。鉴于他在数理统计学方面的突出成就，他曾于1980年以 “线性模型中误差方差估计的相合性” 获中国科学院科技成果奖二等奖，1984年以“数理统计中的若干极限理论问题” 获中国科学院科技成果奖??等奖，1990年以 “关于非参数统计的若干问题” 获中国科学院自然科学奖二等奖，1991年该项目又获国家自然科学奖三等奖。现着重介绍他在几个方面的突出成就。

我国线性回归大样本理论的开拓者

线性回归模型是数理统计学中最重要、应用最广泛的模型，对误差服从正态分布且用最小二乘 (LS) 法进行估计的情况，早已建立了基于精确分布理论的一整套简单易行的小样本方法。为了提高方法的稳定性，最小一乘 (也称最小绝对偏差，LAD)估计、M估计及其他若干估计相继被引进并得到统计界的重视。作为极值问题或方程的解，这些估计没有显式表达，加之应用的广泛性，即使在LS估计的场合也要求突破正态假定的樊篱，这就使得小样本方法无能为力。因此近几十年来大样本理论，即当观察或试验次数趋于无穷时统计方法的极限性质的研究，构成了回归分析研究的主流。

陈希孺是我国最早涉足这个领域的统计学家。这是他投入时间和精力最多的一个领域。自20世纪70年代末至今，他带领学生们在这个领域辛勤耕耘，获得了一系列有根本意义的结果，在一定程度上改变了这个领域的面貌。例如，他最早开展了在高斯-马尔科夫条件下回归系数LS估计的强相合问题的研究，在1979年得出了一个沿着那个方向无可改进的充分条件，最近又与金明仲一起解决了充要条件问题，把它归结为正交级数理论中的一个问题。在误差独立等假定之下，他证得若LS估计不为弱相合，则在排除了某种平凡情况之后，回归系数没有其他的线性弱相合估计，进而又得出了存在非线性弱相合估计的充要条件。在误差独立同分布且只有有限的r阶矩 (1≤r<2) 等条件下，他给出了LS估计为弱相合的充要条件，以及它为强相合的一个充分条件，并证明了这个条件在某种意义上也是必要的，这个问题以往只在误差有二阶矩时解决过。另外，他在最弱的条件 (误差有6阶矩) 下证明了误差方差估计的分布逼近于正态分布的理想的一致速度O(n^-1/2)，国外同行在更强的条件下也未能达到这一速度。在此基础上，他还与他的学生赵林城通过精深的分析，解决了这个逼近的非一致速度等问题。陈希孺等人在这方面的另一项成果是在误差独立但不必同分布的条件下，得出了误差方差估计强、弱相合性的充要条件。

LAD估计的问世与LS估计一样早，但由于没有显式表达，导致了计算理论上的种种困难，使研究长期没有得到开展。直到近年来发现了它与线性规划的联系，加之计算机的使用解决了计算问题，概率极限理论的进展提供了大样本研究的工具，以及对这种估计某些优点的认识，促进了对它的研究。理论上首先要解决的问题是回归系数LAD估计的相合性和渐近正态的条件。70年代以来，学者们针对这些问题发表了许多研究论文，但条件多过于繁复，有的论文在论证中包含有不可改正的错误。陈希孺带领学生们自80年代中期起研究这个问题，他与白志东、赵林城、吴月华在1990年发表的工作中，以一种独创的逐步分割法，在最弱的条件下证得了LAD估计的渐近正态性，其中加在设计点列上的条件d_n趋于零相当于独立和渐近正态理论中的林德伯格(Lindeberg) 条件，因而是无法改进的。熟知，在70年代对LS估计的研究中，一个深刻而优美的结果是：在误差独立同分布，方差非零有限等条件下，回归系数LS估计弱相合与强相合等价，且都等价于S_n^-¹→0，其中矩阵

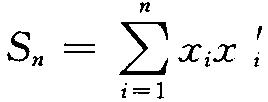，而x_i是p维自变量在第i次观察或试验中的取值。对于LAD估计，强弱相合性已不再等价。通过分析他提出了一个猜测，即LAD估计弱相合的充要条件仍为S_n^-1→0。他及合作者解决了其中p=1的特例，并在p>1时得出了接近于上述猜测的结果。对于它的强相合性，他们得出了一个只依赖于d_n的充分条件，简化和深化了已有结果，并证明了所加条件基本上已无法再改进

M估计是由美国统计学家胡伯在1964年引进的，70年代初被推广到一般的线性模型，它包含了LS和LAD这两类重要估计作为特例，因其包罗之广而备受统计学家重视。作为这个方向上的一大突破，1993年他与赵林城及C.R. 拉奥 (Rao) 合作，在与LS情形相当的条件下 (例如设计点列只需满足S_n^-1→0)，得到了回归系数M估计的弱相合性，涵盖了包括LAD及LS估计在内的广泛情形，以前的作者则加上了更强甚至不易验证的条件。由于M估计没有显式表达，这一证明具有相当的难度。陈希孺等人还给出了回归系数M估计强相合的一些充分条件，其中1988年的一项工作突破了在定义M估计时的凸假定，在很??般的条件下得出了它的强相合性，他们创建的证明方法后来为利泽 (Liese) 和沃伊道 (Vajda) 用来把这些结果推广到非线性回归的M估计。陈希孺对M估计的另一方面的工作是其线性表示。这一研究源于1966年印度统计学家巴哈杜尔关于样本分位数用独立和去强逼近的速度的研究，后来的学者把这一研究拓充到一般线性回归的LAD估计和M估计，但都是在凸假定的前提之下。陈希孺在1993年发表的工作突破了这一限制，取得了很好的逼近速度，并用所得结果导出了M估计的重对数律及依分布收敛于正态的一致速度。

陈希孺及其合作者关于线性回归大样本理论的研究成果，大部分收集在他们撰写的专著《线性模型参数的估计理论》和《线性模型中的M方法》中，并在国外出版物中介绍过。国际著名统计学家拉奥教授等人在其专著中也引述了其中若干重要结果。

在非参数统计领域中的杰出成就

在我国，非参数统计的研究始于张里千先生20世纪50年代关于柯尔莫戈洛夫 (Колмогоров) 和斯米尔诺夫 (Смирнов) 统计量真确分布和渐近展开的工作，以及王寿仁先生和成平先生的有关工作。这一重要分支在国际上一度得到较快发展。从70年代末开始，陈希孺花了不少精力投入这一方向，并影响和带动了一批人。他与其合作者取得了多项重要成果，今择其重要者介绍如下：

一是概率密度的估计问题，以f(x) 和f_n(x) 分别记待估计的密度函数及其基于n个样本的估计量。一个重要的问题是：对一种特定的估计f_n，它在某种意义下收敛于f的速度最高能达到多少，又在不限制估计量的类型时能达到多少。陈希孺在这个问题上获得了一系列精确结果。例如，他在1983年的一项工作中，对f满足δ阶李普希茨 (Lipschitz) 条件的情形，证明了f的近邻估计的一致收敛最优阶的主部为O(n^-δ/(1+3δ)); 在1984年的一项工作中，他在m元密度f的k阶混合偏导数有界的族中，证明了它在任一点的值 (例如f(0)) 的任何估计的均方误差达不到o(n^-2k/(2k+m⁾)，但可以达到O(n^-2k/(2k+m))。他在90年代与其合作者的工作中，分别对直方图估计与核估计的情形，得到了∫|f_n(x)-f(x)|^rdx强收敛于零及E∫|f_n(x)-f(x)|^rdx收敛于零的充要条件 (r≥1)，在以往的文献中只解决了r=1的情形。对f的随机直方图估计f_n，在1987及1990年的两篇文章中，他及合作者在很弱的条件下建立了∫ |f_n(x)-f(x)|^rdx强收敛于零的极限定理，同时建立的关于经验分布的不等式也有独立的意义。他在非参数回归、判别和预测等方面也作出了杰出的工作，在国内统计界起了带头和推动的作用。

他关于非参数统计另一方面的工作涉及一些重要的非参数统计量，包括秩统计量，置换统计量与U统计量，尤以后者为??著。U统计量是美国统计学家霍夫丁在1948年提出的，它是统计学中最常用的统计量算术平均的直接推广，在非参数估计和??验问题中有重要应用，且从纯概率的角度也提供了许多有深度的研究课题，因此备受概率统计学家的重视。在1980年的一项工作中，他在核有r阶矩 (1<r<2) 的假定下，得到了U统计量强收敛及r阶矩收敛速度的确切阶，但更为深刻及重要的成果则在于其分布收敛方面。

1948年霍夫丁在他关于U统计量的奠基性工作中，即已证明了它的渐近正态性，以后有许多学者研究其正态逼近的一致速度。经过30年，到1978年才由卡勒里和简生在核有三阶矩的条件下得到了O(n^-1/2) 的阶。但这个估计从某种意义上说仍嫌粗糙，因为当x趋于无穷时，标准化U统计量的分布F_n(x) 与标准正态分布Φ(x) 之差△_n(x)=|F_n(x)-Φ(x)|趋于零，故在△_n(x) 的更精确的估计中，还应包含一个与x有关的项，这就是所谓 “非一致性估计”。1982年陈希孺与赵林城合作解决了这个问题，在核有三阶矩的条件下证得△n (x)=O(n^-1/2 (1+|x|)^-3)，其中因子 (1+|x|)^-3是无可改进的。这一成果受到国际同行的相当重视，它及稍后赵林城关于学生化U统计量的一项工作均为美国出版的《统计科学百科全书》所引用。由俄罗斯学者柯罗廖克和波罗夫基赫在1989年撰写并译成英文出版的专著 “Theory of U-Statistics”在其导言中介绍本领域重要工作时提到了上述工作，并在书中以8页的篇幅作了仔细的论述。陈希孺与其合作者撰写了这个领域的专著《非参数统计》。除以上两方面之外，陈希孺还涉足过其他统计领域的研究工作，在此不一一仔细介绍了。例如他首先在我国开展了经验贝叶斯 (Bayes) 估计的研究，他证明了国外学者的一个有关的猜测：在一定条件下经验贝叶斯估计的贝叶斯风险与真正的贝叶斯估计的贝叶斯风险的差距不能达到数量级o(1/n)。

综观陈希孺的研究工作，应该说是纯理论性的居多。他自己也曾说过，他研究的是“有统计背景和统计意义的数学问题”。这固然与他的个人气质和学术兴趣有关，也与这门学科在我国发展的历史背景有关。他一直很重视应用研究，鼓励学生们及青年

学者更多地投入统计方法的研究，包括与其他应用学科相结合的边缘领域的研究，认为这应当是未来我国统计学发展的主流。对纯理论性的统计研究，他欣赏和追求的是这样的工作：其假定??单自然，其结论可用简练准确的语言表述，而达到这种结论又有相当的难度，他认为这样的工作具有 “数学美”，这无疑在相当大的程度上成为他选择研究课题的一个准则，他的若干较好的工作也确乎达到或接近这个标准。这反映了他的风格和学术趣味，值得一记。

自1961年1月以来，陈希孺教授一直在中国科学技术大学数学系和北京研究生院数学部工作。作为一名教员，在 “文化大革命”前他主要的时间是花在教学上的; 80年代以后，在致力于研究及著述的同时，除了带研究生以外，还在若干统计讲习班上担任主讲，从1979年到1983年的5年中，每年暑期主持为时1个月的全国性的统计讲习班，并多次应邀在各地举办的班上讲课，讲的内容有补基础的，有关于某些研究专题的。如1979年在武汉和开封，1980年在广州，1981年在九江，1983年在屯溪，1984年在成都，1986年在郑州等，这些活动的参加者主要是中青年教师和科研人员。数理统计学本是我国数学中的薄弱分支，又经过 “文化大革命” 10年的停顿，到70年代后期队伍已很衰微，陈希孺在这时及后来所进行的上述活动，引进和推广了这个分支若干重要领域的研究成果，带领、培养和联系了一批人投入研究工作。他在学术上很乐于给人以力所能及的帮助。目前我国数理统计界的骨干队伍中，不少人在早期就与他有联系，并曾在进入研究工作的阶段得到过他的指导和帮助。他先后带出了10位博士，大多数已成为学科带头人和业务骨干，活跃在科研和教学的第一线。一些人取得了具有国际影响的成果，其中白志东已成为第三世界科学院院士。在陈希孺撰写的11本专著及教科书中，最早的一本即1981年的《数理统计引论》，印数近万册。该书用严格的数学理论对现代数理统计基础的主要方面作了仔细的论述，材料充实，出版后一直被广泛地采用为研究生教材，在青年教师和研究人员中也拥有许多读者。该书无疑是国内撰写的统计著作中影响最大者之一，也可算作陈先生对我国统计教育的一项贡献。

他淡泊名利，主张顺乎自然，他喜欢的格言是 “尽人事以俟天命”。他常说，不少人在这个问题上修养不到家，碰到了很多麻烦，甚至毁了一生，他常以此告诫他的学生。他在逆境中也能安之若素。他的学生和同事有什么不顺心的事，愿意和他谈心，他也往往以自己的切身体会去劝导他们。他能容人，也乐于助人。他的主要爱好是读书，读书多且面广，故对许多事都能谈出自己的见解。他还爱好登山涉水，登临过国内若干名山之顶，如今虽年过花甲，仍乐此不疲。

简历

1934年2月11日出生于湖南省望城县。

1956年9月毕业于武汉大学数学系。

1956年9月—1960年12月在数学所任实习研究员。

1957年10月—1958年10月在波兰科学院数学所进修。

1959年3月—1960年1月下放陕西洛川劳动。

1961年1月在中国科技大学数学系，先后任助教、讲师 (1963年)、副教授 (1978)、教授 (1980)，1981年为博士生导师。

1986年4月在中国科技大学研究生院任教授。

1986年7月—1988年5月在加拿大Manitoba大学和Pittsburgh大学做访问学者。

1984—1986年任中国数学会概率统计学会理事长。

1983—1987年任中国数学会理事。

1991—1996年任中国科协全国委员会委员。

1993—2005年任中国现场统计研究会理事长。

2005年8月8日在北京逝世。

主要论著

1 陈希孺. 数理统计引论. 北京：科学出版社，1981

2 陈希孺，陈桂景，吴启光，赵林城. 线性模型参数的估计理论. 北京：科学出版社，1985

3 陈希孺，王松桂. 近代回归分析. 合肥：安徽教育出版社，1987

4陈希孺，方兆本，李国英，陶波. 非参数统计. 上海：上海科学技术出版社，1989

5 陈希孺，赵林城. 线性模型中的M方法. 上海：上海科学技术出版社，1996

6 Chen Hsi-ju. On minimax invariant estimation of scale and location parameters. Scientia Sinica. 1964，13 (10)： 1369—1384

7 陈希孺. 关于U统计量和von-Mises统计量的极限性质. 中国科学.1980，10 (6)： 522—532

8 陈希孺. 线性模型中误差方差估计的Berry-Esseen界限. 中国科学.1981，11 (2)： 129—140

9 陈希孺. 最近邻密度估计的收敛速度. 中国科学，1981，11 (12)：1419—1428

10 赵林城，陈希孺. U统计量的分布的非一致性收敛速度. 中国科学A辑. 1982，12 (12)： 1066—1078

11 Chen Xiru. On one conjecture of Singh. Chin. Ann. of Math.，1983，4B (2)： 183—188

12 Chen Xiru. Exponential posterior error bound for the kNN discrimination rule. Scientia Sinica，Ser. A. 1985，28 (7)： 675—682

13 Chen Xiru. Zhao Lincheng. The optimal rate of error for kNN median regression estimates. Chin. Ann. of Math.，1986，7B (2)：129—138

14 Chen，X. R.，Zhao，L. C. Almost sure L1-norm convergence for data-based histogram density estimates. J. Multivariate Anal.，1987，21(1)： 179—188

15 Chen Xiru. Inference in a simple change point model. Scientia Sinica，Ser. A.，1988，31 (6)：654—667

16 Chen，X. R.，Wu，Y. Strong consistency of M-estimates in linear models. J. Multivariate Anal.，1988，27 (1)：116—130

17 陈希孺，白志东，赵林城，吴月华. 线性模型中最小一乘估计的渐近正态性. 中国科学A辑. 1990，20 (5)： 449—463

18 Zhao，L. C.，Krishnaiah，P. R.，Chen，X. R. Almost sure Lrnorm convergence for data-based histogram density estimates. Theory Probab. Appl.，1990，35 (2)： 391—397

19 Zhao，L. C.，Rao，C. R.，Chen，X. R. A note on the consistency of Mestimates in linear models. Stochastic Processes (ed. S. Cambanis et al.). New York： Springer，359—367

20 陈希孺. 线性回归M估计的线性表示. 中国科学A辑. 1993，23(12)： 1264—1275

21 Chen，X. R，Wu，Y. Consistency of L1 estimates in censored linear regression models. Commun. Statist. -Theory Meth.，1994，23 (7)：1847—1858

22 陈希孺. 低阶矩条件下线性回归最小二乘估计弱相合的充要条件. 中国科学A辑. 1995，25 (4)： 349—358

23 Chen Xiru. On a problem of strong consistency of least absolute deviation estimates. Statistica Sinica. 1996，6 (2)：481—489

知名人物 陈希孺人物简介

知名人物 陈希孺人物简介

·陈希孺

知名人物陈希孺人物简介

知名人物陈希孺人物简介